More than a Pulley Problem...
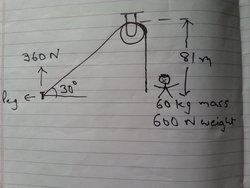 A rope that's fixed to a peg in the ground goes around a pulley making an angle of 30 degrees to the ground.
A rope that's fixed to a peg in the ground goes around a pulley making an angle of 30 degrees to the ground.
Anand, who weighs mass 60 kg, is at the other end of the rope and wants to climb up this rope to the top, 81 meters, as fast as possible.
The peg in the ground will be uprooted if a Force exceeding 360 N is applied vertically upward to it.
Taking g = 1 0 m/s 2 , what is the minimum time in seconds that Anand will take to safely clamber up the rope to the top?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
For Anand to be held stationery, a Tension force of 600N vertically upwards must be sustained. Since the rope over the pully is one rope, we treat the tension in it equally. so the tension pulling on the Peg would be 600. If we get the 2 components by resolution, the vertical force is:
6 0 0 sin 3 0 = 3 0 0 N s o t h e f o r c e A a n a n d c a n a p p l y c a n o n l y a f f e c t t h e p e g b y a m a x i m u m o f 6 0 N . B u t r e m e m b e r t h a t a n y f o r c e h e a p p l i e s i s g o i n g t o b e m u l t i p l i e d b y sin 3 0 = 2 1 . T h i s t r a n s l a t e s t o : X sin 3 0 = 6 0 . X = 1 2 0 N W e t h e n u s e F = m a t o g e t 1 2 0 = 6 0 a a = 2 m s 2 N o w u s i n g K i n e m a t i c s u = 0 , a = 2 , s = 8 1 , t = z s = u t + 2 1 a t 2 S u b s t i t u t i n g i n V a l u e s : 8 1 = t 2 t = 9 s e c o n d s
The total force on Anand is Fu:
Fu = Ft - Fw;
by the force Fu Anand accellerate upward,
Fw is the weight force of Anand, Ft the total tension on the rope;
Fv = 360 N is the maximum vertical vincular reaction of the peg,
Ft = Fu + Fw = ma + mg = m(a + g); (1)
for the equilibrium on the peg:
Fv/sinθ > Ft; Ftsinθ < Fv; (with θ = 30°) (2)
the height h is:
h = (1/2)at^2; so: a = 2h/(t^2); (3)
combining (1) and (3) in (2) we obtain:
m(2h/(t^2) + g)sinθ < Fv; which leads to:
t > √(2h/(Fv/(msinθ) - g));
- Hypotesis: g ~ 10 m/s; Fv = 360 N; m = 60 Kg; θ = 30°; h = 81 m;
t > √(2 x 81/(360/(60 x 1/2) - 10)) = √(2 x 81/(720/60 - 10));
t > √(2 x 81/(12 - 10)) = √(2 x 81/2) = 9 = tmin (ANSWER)
Hi am anand :D
Answer is sqrt(2 81/360 60) = 9 seconds
The maximum tension on the rope should be 720N [360/cos60] Anand weight is 600N, so he can pull hisself with 120N up. F=m . a, 120 = 60 . a, a=2 Y= vt +1/2 at^2, 81=1/2.2t^2, t= 9sec.
The max force that the peg can take is given by 360 N/ sin 30= 720 N.
Anand with weight 600 N thus has 120 N to use for accelerating upwards. F= ma
120=60*a
a = 2 m/s^2
Using equation of motion,
s= ut +1/2 at^2
81= t^2
t = 9 seconds.