More than one way to solve
A rectangle has the following vertices: A ( 0 , 0 ) , B ( 1 0 , 0 ) , C ( 1 0 , 5 ) , D ( 0 , 5 ) . We want to circumscribe an ellipse about the rectangle, that is, an ellipse passing through these four vertices. There is an infinite number of ellipses satisfying this property. Find the one with minimum area. If that minimum area can be expressed as n π , for a positive integer n , then enter n as your answer.
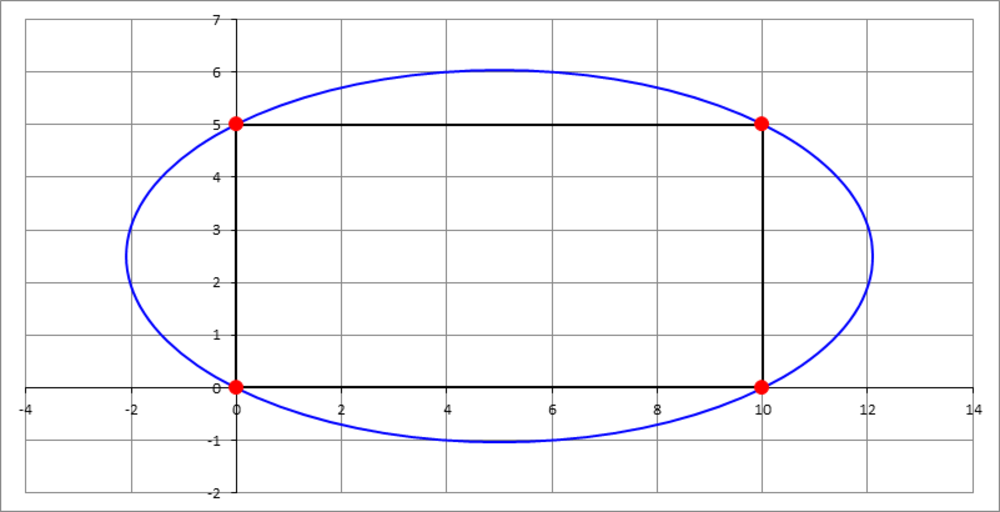
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Denote the center of the ellipse as E. We know that the horizontal distance from E to any of A, B, C, or D is equal to 5. Likewise, we know that the vertical distance from E to any of A, B, C, or D is equal to 2.5. Therefore, point E is located at (0 + 5, 0 + 2.5) = (5, 2.5).
The equation for the ellipse cirumscribed around rectangle ABCD is: a 2 ( x − 5 ) 2 + b 2 ( y − 2 . 5 ) 2 = 1 All points A, B, C, and D must satisfy the above equation. If we select any of these points, we will get the following relationship between a and b : a 2 2 5 + b 2 6 . 2 5 = 1 And solving for a gives us: a = 1 − b 2 6 . 2 5 2 5 = b 2 − 6 . 2 5 2 5 b 2 = 5 b b 2 − 6 . 2 5 1
The area of any ellipse is A = π a b meaning the area of our ellipse is A ( b ) = 5 π b 2 b 2 − 6 . 2 5 1 . We wish to find the value of b which minimizes the ellipse's area - that is, we wish to find the values of b where A ′ ( b ) = 0 and ( b , A ( b ) ) is a minimum. Using the product rule, A ′ ( b ) is equal to: A ′ ( b ) = ( b 2 − 6 . 2 5 ) 2 1 1 0 π b − ( b 2 − 6 . 2 5 ) 2 3 5 π b 3 And further simplifying into a single term: A ′ ( b ) = ( b 2 − 6 . 2 5 ) 2 3 1 0 π b ( b 2 − 6 . 2 5 ) − ( b 2 − 6 . 2 5 ) 2 3 5 π b 3 A ′ ( b ) . = ( b 2 − 6 . 2 5 ) 2 3 5 π b 3 − 6 . 2 5 ⋅ 1 0 π b Note that A ′ ( b ) can only equal zero when the numerator 5 π b 3 − 6 . 2 5 ⋅ 1 0 π b equals zero. 5 π b 3 − 6 . 2 5 ⋅ 1 0 π b = 0 b = ± 5 π 6 . 2 5 ⋅ 1 0 π = ± 2 5 2 b = 0 would also be a valid solution to this equation, however, an ellipse with a vertical lengh of 0 would not be able to intersect with any of the corners of rectangle ABCD. Since there are only two critical points and b = − 2 5 2 is unreasonable (for the same reason that b = 0 is unreasonable), we know that a value of b = 2 5 2 yields the minimum value for the area of the ellipse. We know that b yields the minimum area of the ellipse since it is impossible for the ellipse to have a maximum area (the ellipse can extend indefinitely in the y direction). Substituting this value for b into A ( b ) returns an area of 2 5 π meaning that the answer to the problem is 2 5
The center of the ellipse is at the center of the rectangle ( 5 , 2 . 5 ) , hence its equation is
a 2 ( x − 5 ) 2 + b 2 ( y − 2 . 5 ) 2 = 1
Plugging in one of the four vertices, (from symmetry, one vertex is sufficient) we get,
a 2 2 5 + b 2 6 . 2 5 = 1
We're seeking the minimum of a b , i.e. the maximum of a b 1 . Using AM-GM, we have
1 = 2 ( 1 / 2 ) ( a 2 2 5 + b 2 6 . 2 5 ) ≥ 2 a 2 b 2 ( 2 5 ) ( 6 . 2 5 ) = a 2 b 2 2 5 2 = a b 2 5
Hence, a b ≥ 2 5 , and thus the minimum area of the circumscirbed ellipse is 2 5 π and n = 2 5 .
By symmetry, the ellipse with the minimum area that passes through the four vertices of square A B ′ C ′ D , with B ′ ( 5 , 0 ) and C ′ ( 5 , 5 ) , would be a circle.
The diameter of this circle is the same as the diagonal of the square, which is d = 5 2 , which means its radius is r = 2 5 2 .
Stretching this square and circle horizontally by a factor of 2 would give rectangle A B C D and the ellipse with the minimum area, which has a semi-major axis of a = 2 r and a semi-minor axis of b = r .
The area of this ellipse is A = a b π = 2 r 2 π = 2 ( 2 5 2 ) 2 π = 2 5 π . Therefore, n = 2 5 .