More tic-tac-toe!
How many tic tac toe games can be played wherein O starts the game and the game has to end in a draw?
Rotations of the game are considered distinct, so a game with an O at the top right corner is different with one at the top left corner. Also, the players will not necessarily play perfectly!
Clarification : "Playing" the game means the actual order in which both players put their pieces count.
The answer is 46080.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Please state that we must assume rotations result in different games. I thought otherwise and since have gotten the question incorrect.
@Manuel Kahayon If both the players play 'perfectly' to win, then a lot of those 2880 ways for each of those positions get eliminated. 2880 * 16 is only possible if both players don't play perfectly, but play just to create a possibility. Could you include this in the problem statement?
Relevant wiki: Permutations - Problem Solving
Having a draw in the game of tic-tac-toe means that our 3×3 grid is filled with 5 circles and 4 crosses, in a way that there aren't any 3 crosses or circles that form a row, a column or a diagonal.
There are 9! ways to fill a 3×3 grid with 5 circles and 4 crosses in total.
As there are 3 rows, 3 columns and 2 diagonals (3 + 3 + 2 = 8 key triplets altogether), the number of cases when we have (at least) one of these key triplets
a) made out of crosses is:
8 × ( 1 6 ) = 4 8
b) made out of circles is:
8 × ( 2 6 ) − 9 − 1 2 − 1 = 9 8 , since
there are 8 key triplets, then we have to choose 2 places out of 6 for the remaining two circles and deduct those ways, which we counted twice, as 5 circles can form:
-
a row and a column in 9 cases
-
a row/column and a diagonal in 6 + 6 = 12 cases
-
both diagonals in 1 case,
c) both (double counted):
This can only happen, if we have either two rows or two columns made out of rows/crosses (one each). This can be achieved in ( 2 3 ) × 2 × 2 = 1 2 ways, and we can choose the the positions of the remaining 2 circles out of 3 places.
The number of relevant cases:
1 2 × ( 2 3 ) = 3 6
Therefore, we have
98 + 48 - 36 = 110 cases altogether.
As we can occupy the 5 circle / 4 cross positions in any order, the total number of ways to fill the 3 × 3 grid with five circles and four crosses (without considering, whether it is a valid tic-tac-toe game or not) is:
110 × 5! × 4! = 316800 ,
and the number of tic-tac-toe games ending in a draw is:
9 ! − 3 1 6 8 0 0 = 4 6 0 8 0
Maybe you should put your observation that , the cases considered by you do not have to necessarily be valid tic-tac-toe games at the beginning of your proof to make clearer your reasoning and what you are looking for anyway.
Nonetheless this is cute solution but maybe it is also interesting to consider the case of all valid tic-tac-toe games and compare the method of proof between this particular case of calculating the draws and the one for all the games.
good question! got 28 cases where O didn't win without thinking whether x wins or not. X can only win when it is on a diagonal.So total 12 cases where X wins on the diagonal and O doesnt win.Hence total cases will 28-12=16.Then multiply it by 5!4!=2880.So total ways=16*2880=46080
Moderator note:
Several missing steps in your presentation
- Be clearer about what your cases are
- Explain what the calculations are. In particular, how did you get 28? By tediously listing?
- Explain the logic of your steps. In particular, explain why "X can only win when it is on a diagonal" since X could win by having 3 horizontally (without further conditioning)
We first count the number of drawing positions.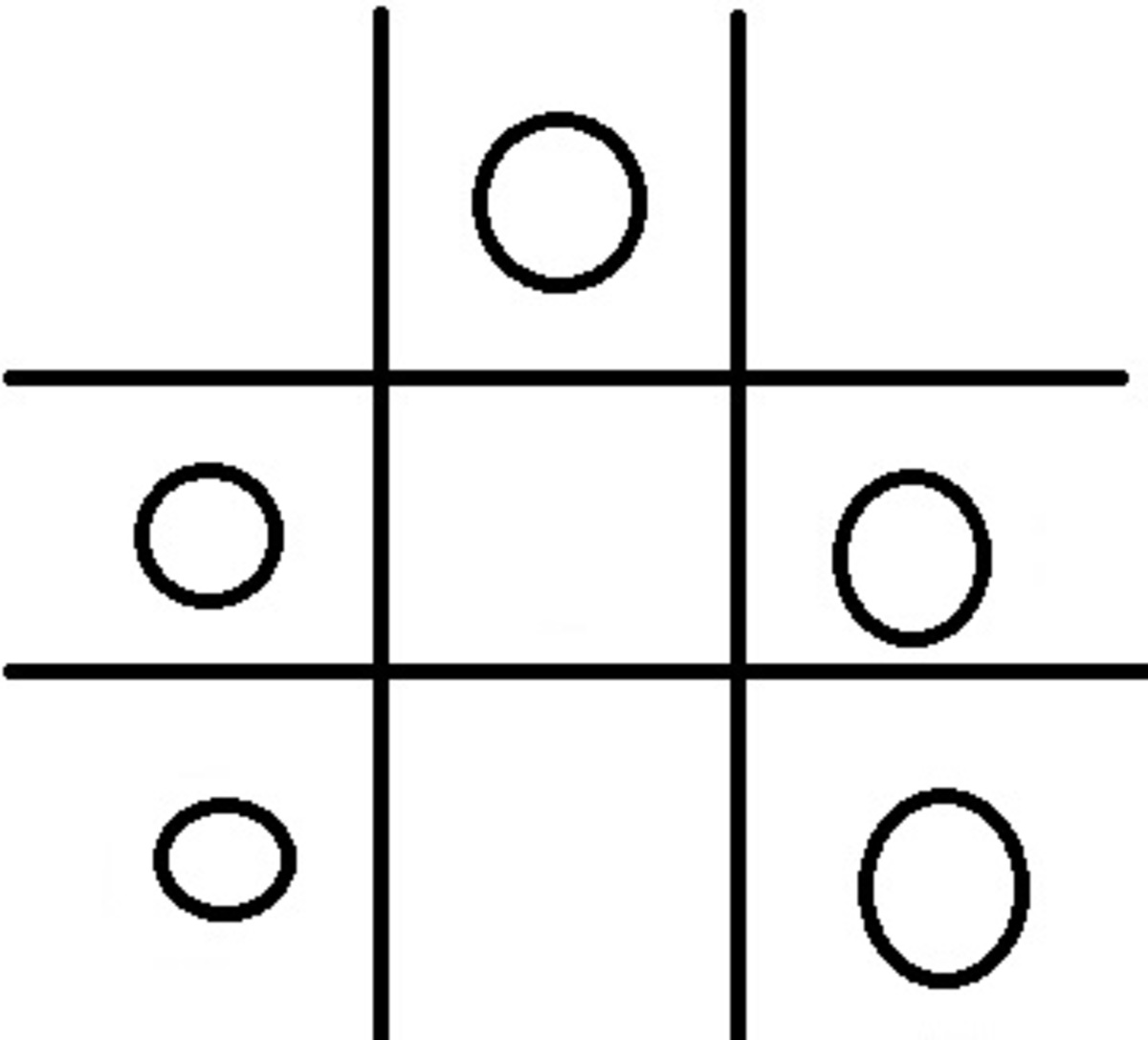
This is a drawing position with 4 rotations. Assume the blank spaces are X 's.
This is a drawing position with 4 rotations. Assume the blank spaces are X 's.
This is a drawing position with 4 rotations and 2 reflections, thus 8 permutations. Assume the blank spaces are X 's.
Therefore, the total number of drawing positions are 8 + 4 + 4 = 1 6 . But, notice that in any given position, O can choose any of the 5 O 's to put in the grid first. Similarly, X can put his next X in 4 ways, and so, on, so the number of ways to acquire any given position is 5 ! 4 ! = 2 8 8 0 .
But, there are 1 6 positions, so the total number of ways to play a drawing game is 1 6 ⋅ 2 8 8 0 = 4 6 0 8 0 .