More Wrecked Angles
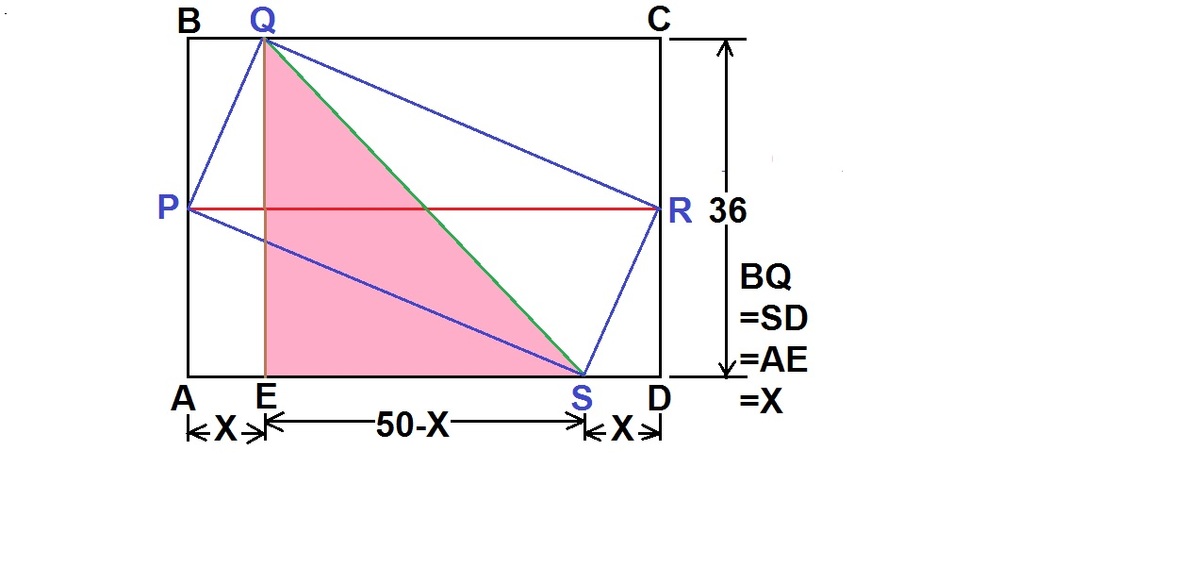
In the diagram above, ABCD and PQRS are both rectangles. Points P , Q , R , and S lie on segments A B , B C , C D , and D A , respectively, and B Q < Q C .
If A B = 3 6 and B C = 5 0 , then the maximum possible value of B Q can be written in the form a − b , where a , b ∈ N . What is a + b ?
The answer is 326.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
 L
e
t
Q
E
⊥
A
D
w
i
t
h
E
o
n
A
D
.
Let BQ=SD=AE=X.
BQ increases as diagonal QS decreases. But diagonal PR
≮
5
0
.
But diagonals of a rectangle are equal (and bisect one another).
⟹
m
i
n
i
m
u
m
Q
S
≮
5
0
.
So from the sketch,
Q
S
2
=
Q
E
2
+
E
S
2
⟹
5
0
2
=
3
6
2
+
(
5
0
−
2
X
)
2
.
∴
X
=
2
1
{
5
0
−
5
0
2
−
3
6
2
}
.
=
a
−
b
.
∴
a
+
b
=
3
2
6
L
e
t
Q
E
⊥
A
D
w
i
t
h
E
o
n
A
D
.
Let BQ=SD=AE=X.
BQ increases as diagonal QS decreases. But diagonal PR
≮
5
0
.
But diagonals of a rectangle are equal (and bisect one another).
⟹
m
i
n
i
m
u
m
Q
S
≮
5
0
.
So from the sketch,
Q
S
2
=
Q
E
2
+
E
S
2
⟹
5
0
2
=
3
6
2
+
(
5
0
−
2
X
)
2
.
∴
X
=
2
1
{
5
0
−
5
0
2
−
3
6
2
}
.
=
a
−
b
.
∴
a
+
b
=
3
2
6
The centroids of the rectangles are concurrent (Why?) - call this point O. Since PQRS is a rectangle, its diagonals are congruent, bisect eachother, and intersect at O. The length of half a diagonal OQ decreases when the length of BQ increases. Since OQ=OP and P is on AB, the shortest OP can be is 25, We investigate this case: consider the right triangle with two vertices Q and O and with one leg including Q parallel to AB. The leg parallel to BC would have length \sqrt{301}, so the length of BQ is 25 - \sqrt{301}.
Moderator note:
Great analysis! A simple argument which shows that the minimum occurs when P is the midpoint of AB.
Another simple argument would be to draw a circle centered at the center of ABCD that intersects ABCD in 4 places, PQRS, which will always form a rectangle. Then maximum BQ would occur with the smallest radius this circle can have, which would be if P and R are midpoints of AB and CD.
Helpful way to think of this is you have a circle centered at the center of the rectangle and PQRS are its intersections with the rectangle. With a little thought BQ=25-SQRT(r^2-18^2) where r is the radius of this circle. The minimum value of r is half the length of the rectangle from A to D if it is to intersect all 4 sides. So the max value of this happens when r=25 and from that we get 25-sqrt(301)
Write P = ( 0 , y ) , Q = ( x , 3 6 ) , R = ( 5 0 , 3 6 − y ) , S = ( 5 0 − x , 0 ) . For P Q R S to be a rectangle, we must have slope ( P Q ) ⋅ slope ( Q R ) = − 1 . Thus, − 1 = x 3 6 − y ⋅ x − 5 0 y = x 2 − 5 0 x 3 6 y − y 2 , and so, y 2 − 3 6 y = x 2 − 5 0 x ( y − 1 8 ) 2 = ( x − 2 5 ) 2 − 3 0 1 y = 1 8 ± ( x − 2 5 ) 2 − 3 0 1 . So, if ( x , y ) ∈ R 2 , we must have ( x − 2 5 ) 2 − 3 0 1 ≥ 0 , or ∣ x − 2 5 ∣ ≥ 3 0 1 .
Finally, B Q < Q C ⟹ x < 2 5 , so ∣ x − 2 5 ∣ = 2 5 − x , and B Q = x ≤ 2 5 − 3 0 1 .
Moderator note:
Having worked through to obtain the answer, is there any insight that you can gleam from your work to find a better explanation?
Hint: In the ideal case, where does point P lie? Why?
it lies midway AB.
 x=25 - SQRT(301), A + B= 25 +301=326
x=25 - SQRT(301), A + B= 25 +301=326
Sorry, spent a lot of time, trying to load an image on Imgur and get the link to embed it here. But it just did not work. Is there some other way of doing it?
Let (f : 1-f) be the ratio in which P divides AB. This will be repeated by point R on the opposite side CD as (1-f : f). By symmetry, the midpoint of PR always remains at the center (O) of ABCD.
Now, if we use these pairs of points P & R as the diameter for various values of f, we will get a family of concentric circles that intersect BC at points Q. And smaller the circle gets further Q will be from B.
The smallest circle is had (or the closest P & R get) is when P & R are midpoints of AB and CD respectively. This gives radius = OQ = 25 and B Q = 2 5 − 2 5 2 − 1 8 2
Hence a = 25, b = 301 and a + b = 3 2 6