More x(s), more difficult, but not impossible, although.
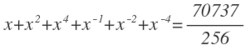 What integer best fits in x?
What integer best fits in x?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I saw the denominator of the RHS as 256, and so I guessed four, but here's the solution.
Let a = x + x 1
x 2 + x 2 1 = ( x + x 1 ) 2 − 2 = a 2 − 2
x 4 + x 4 1 = ( x 2 + x 2 1 ) 2 − 2 = ( ( x + x 1 ) 2 − 2 ) 2 − 2 = ( a 2 − 2 ) 2 − 2
This you then substitute in the given equation, which becomes a degree four equation in a , and once we have the value of a , we can form a quadratic equation in x and obtain the answer, 4 .
Often ...after quickly solving prblm by reosonable guesses and then formulating a solution on the paper is becoming very popular in this culture of prblm solving .. I too did the same in this one ...:)
To quickly deduct the answer I jst saw the lrgest denominatr in the LHS ...which is in fact the LCM
Clearly it is x 4 and is equal to 256
Now We see 2 5 6 1 / 4 = 4
So the answer is 4
Since the R H S = 2 5 6 7 0 7 3 7 ≫ 1
⇒ x 4 ≈ 2 5 6 7 0 7 3 7 ⇒ x ≈ 4 2 5 6 7 0 7 3 7 = 4 . 0 7 7 1 ≈ 4