More Zigzags
Points , , , , , , , , and are on a circle such that and . Which area is greater?
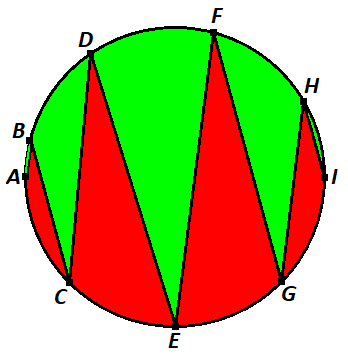
Bonus: Generalize a solution for any angle , where is a positive integer greater than .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Draw I G and consider △ G H I . Let O be the center of the circle with a radius of 1 . Since ∠ G H I = 2 2 . 5 ° , central angle ∠ G O I = 4 5 ° . Draw the perpendicular bisector of G I at J , and draw H K ⊥ O J at K , and let x = ∠ H O I .
Then ∠ I O J = 2 2 . 5 ° , so that from △ I O J we have I J = sin 2 2 . 5 ° and O J = cos 2 2 . 5 ° , and from △ H O K we have O K = cos ( x + 2 2 . 5 ° ) . Therefore, J K = cos 2 2 . 5 ° − cos ( x + 2 2 . 5 ° ) and G I = 2 sin 2 2 . 5 ° , so that △ G H I has an area of A △ G H I = 2 1 ⋅ G I ⋅ J K = sin 2 2 . 5 ° ( cos 2 2 . 5 ° − cos ( x + 2 2 . 5 ° ) ) .
Since inscribed angles ∠ A B C = ∠ B C D = ∠ C D E = ∠ D E F = ∠ E F G = ∠ F G H = 2 2 . 5 ° , central angles ∠ A O C = ∠ B O D = ∠ C O E = ∠ D O F = ∠ E O G = ∠ F O H = 4 5 ° . Then by a similar method from above, A △ E F G = sin 2 2 . 5 ° ( cos 2 2 . 5 ° − cos ( x + 2 2 . 5 ° + 9 0 ° ) ) , A △ C D E = sin 2 2 . 5 ° ( cos 2 2 . 5 ° − cos ( x + 2 2 . 5 ° + 1 8 0 ° ) ) , and A △ A B C = sin 2 2 . 5 ° ( cos 2 2 . 5 ° − cos ( x + 2 2 . 5 ° + 2 7 0 ° ) ) .
That means the sum of the areas of the red triangles is A = sin 2 2 . 5 ° ( cos 2 2 . 5 ° − cos ( x + 2 2 . 5 ° ) ) + sin 2 2 . 5 ° ( cos 2 2 . 5 ° − cos ( x + 2 2 . 5 ° + 9 0 ° ) ) + sin 2 2 . 5 ° ( cos 2 2 . 5 ° − cos ( x + 2 2 . 5 ° + 1 8 0 ° ) ) + sin 2 2 . 5 ° ( cos 2 2 . 5 ° − cos ( x + 2 2 . 5 ° + 2 7 0 ° ) ) = 4 sin 2 2 . 5 ° cos 2 2 . 5 ° , which is equivalent to the sum of the areas of congruent triangles △ A O C , △ C O E , △ E O G , and △ G O I , which means the red area is half the circle, which means the two areas are equal .
The solution above is for the specific case of inscribed angles of 4 9 0 ° = 2 2 . 5 ° where n = 4 . The same method can be used for a more general solution for inscribed angles of n 9 0 ° where n is a positive integer greater than 1 , to find that one set of same-colored triangles have an area sum of k = 0 ∑ n − 1 sin ( n 9 0 ° ) ( cos ( n 9 0 ° ) − cos ( n 9 0 ° + x + k n 1 8 0 ° ) ) = n sin ( n 9 0 ° ) cos ( n 9 0 ° ) , which is equivalent to the area of half a regular polygon with 2 n sides, to conclude that the two areas are equal for any integer n > 1 .