Mortal Kombat

No matter what happens in the first match, Melody finds herself as the "new player", $N,$ against a winner, $W,$ with a third person as a loser, $L.$ Let $P_{*}$ be the probability that a person currently in state $*$ wins the tournament.

For the "loser" to win, they first need the "new player" to win (else the tournament would end). Then, they become the "new player": $P_{L} = \frac{1}{2} \cdot P_{N}$

For the "new player" to win, they first need to win the match against the "winner". Then, they become the "winner": $P_{N} = \frac{1}{2} \cdot P_{W}$

For the "winner" to win, they can either win immediately, or if they lose they become the "loser": $P_{W} = \frac{1}{2} + \frac{1}{2} \cdot P_{L}$

Solving these three equations gives $P_N = \frac{2}{7}.$

The following probability tree can be constructed to describe the possible outcomes of the tournament, where D represents a match that Danielle wins, L represents a match that Lilliana wins, and M represents a match that Melody wins:

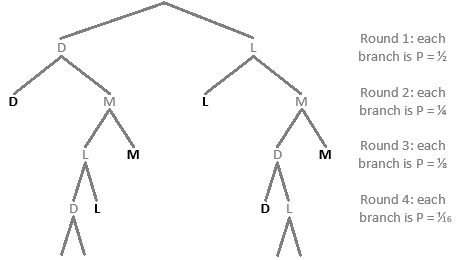
In Round 3, where each branch is worth $\frac{1}{8}$ , Melody can win the tournament in 2 possible ways, for at least a 2( $\frac{1}{8}$ ) = $\frac{1}{4}$ probability. In Round 4, where each branch is worth $\frac{1}{16}$ , the tournament can continue on to repeat itself, giving Melody another chance to win later on, in 2 possible ways, at a 2( $\frac{1}{16}$ ) = $\frac{1}{8}$ probability. Therefore, the probability P that Melody can win the tournament can be expressed by the infinite expression

P = $\frac{1}{4}$ + $\frac{1}{8}$ ( $\frac{1}{4}$ + $\frac{1}{8}$ ( $\frac{1}{4}$ + $\frac{1}{8}$ (…

Substituting P into the above equation gives

P = $\frac{1}{4}$ + $\frac{1}{8}$ P

and solving this equation for P gives P = $\frac{2}{7}$ or P = 0.285714286.

Danielle wins with probability $d$ , Lilliana with $l$ , and Melody with $m$ . Since Danielle and Liliana play the first match: $d = l$ , and since somebody does win eventually: $d + l + m = 1$ , so $m = 1 - (d + l)$ . Following probability tree, I get this expression for the probability of either Danielle or Lilliana winning:

$2 \, (\frac{1}{2^2} + \frac{1}{2^4} + \frac{1}{2^5} + \frac{1}{2^7} + \frac{1}{2^8} + \frac{1}{2^{10}} + \frac{1}{2^{11}} + \ldots)$

With gaps at powers $3, 6, 9, \ldots$ , the expression constitute of two geometric series that sum to $5 / 7$ , so $c = 2 / 7$ .

Melody doesn't care who wins the first match. But once she play she must win her first game. On the next game she can either win or lose.

If she wins the game end, but if she loses, this new player must lose his next game (or he won the game and Melody lost). At this stage we are at the same position as her first game.

$M=\frac{1}{2}(\frac{1}{2}+\frac{1}{2}*\frac{1}{2}*M)$

So $M=\frac{2}{7}$