Mossy Easter Egg Sangaku

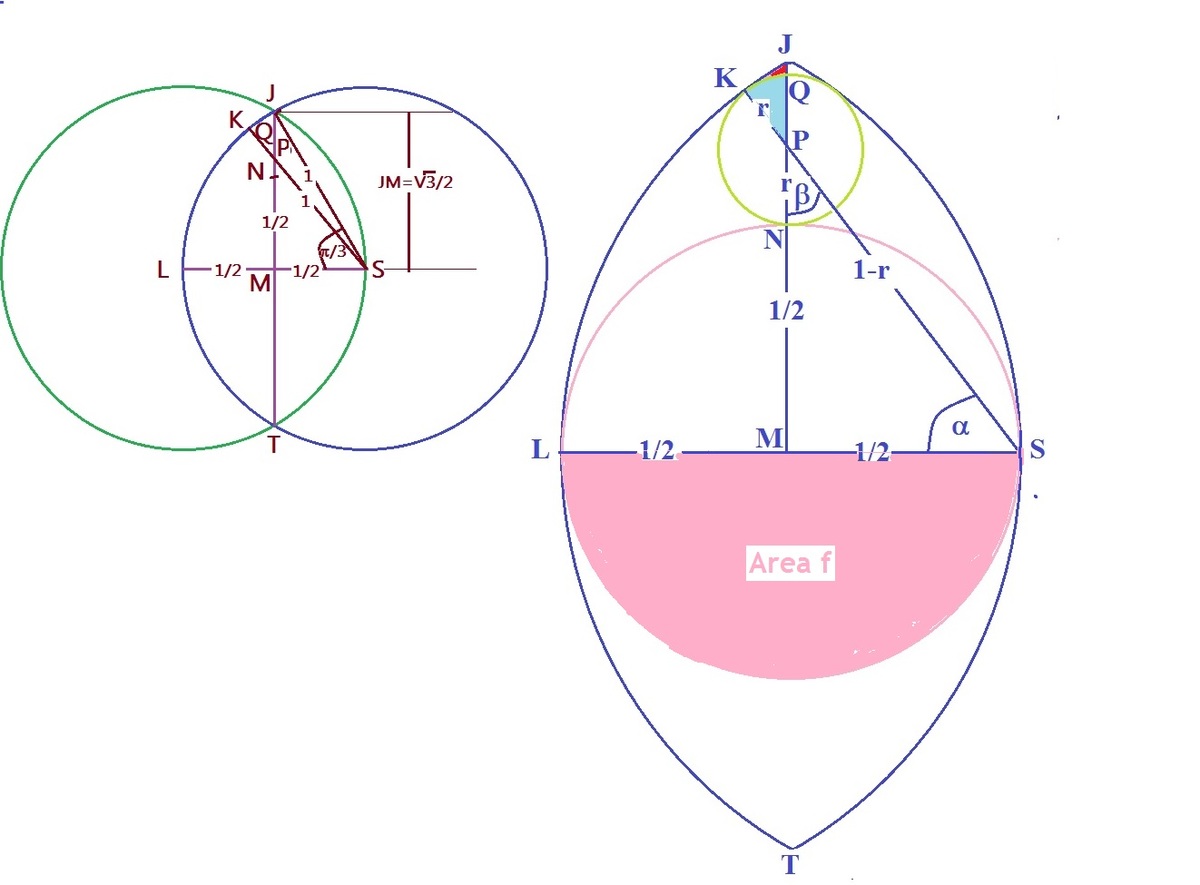
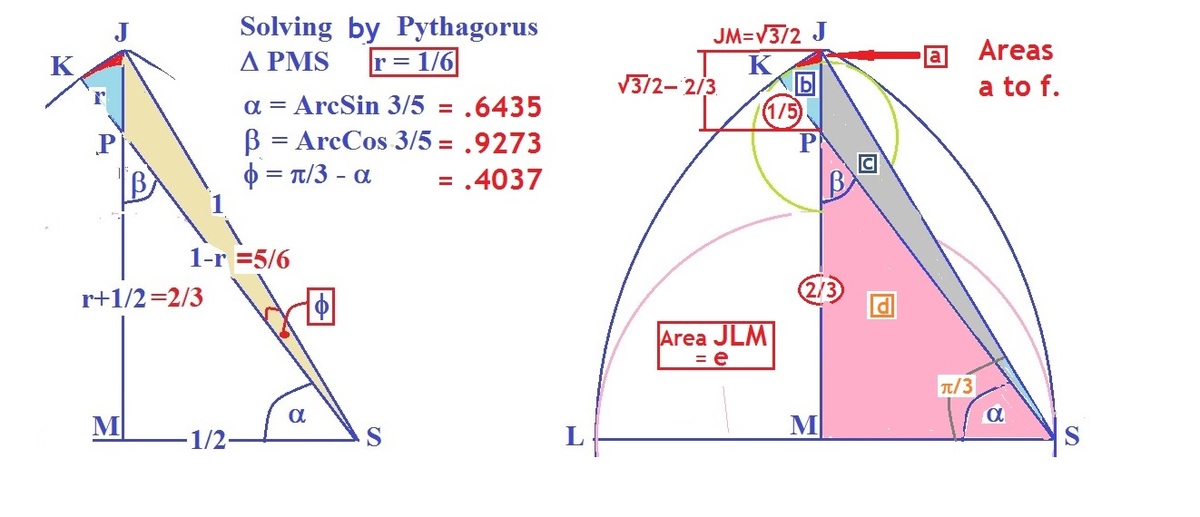
If $r$ is the radius of the smallest circle, then $AB = \tfrac12$ , $BD = \tfrac12+r$ , $AD = 1-r$ . Pythagoras tells us that $r = \tfrac16$ , and hence that $\sin\alpha = \tfrac35$ , where $\alpha = \angle BDC$ .

The small sector $DEF$ has area $\tfrac12 \times 2\alpha \times \tfrac{1}{36} = \tfrac{1}{36}\alpha$ . The big sectors $ACE$ and $FAC$ both have area $\tfrac12(\tfrac12\pi-\alpha)1^2 = \tfrac14\pi -\tfrac12\alpha$ . The triangle $ADC$ has area $\tfrac13$ . Thus the curved region $ABCFE$ has area $\tfrac{1}{36}\alpha + 2\big(\tfrac14\pi - \tfrac12\alpha\big) - \tfrac13 \; = \; \tfrac12\pi - \tfrac13 - \tfrac{35}{36}\alpha$ and hence the desired shaded region has area $\tfrac12\pi - \tfrac13 - \tfrac{35}{36}\alpha + \tfrac18\pi \; = \; \tfrac58\pi - \tfrac13 - \tfrac{35}{36}\sin^{-1}\tfrac35 \; = \; \boxed{1.00454}$

No question Mr. Mark Hennings solution is much much better. However just to give another approach I have posted mine.