Most beautiful problem
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x + x 2 + y 2 3 x − y y − x 2 + y 2 x + 3 y = = 3 0
Solve the system of equations for real values of ( x , y ) , and submit the sum of all values of ( x , y ) .
ie. If you have got pairs as ( 9 , 1 0 ) , ( 5 , 7 ) submit your answer as 9 + 1 0 + 5 + 7 .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great solution hats of to my thoughts
After looking at the solutions above and the ordered pairs they ended up with, I am having doubts about mine. Could someone please explain where I am going wrong?
x + x 2 + y 2 3 x − y = 2 a n d y − x 2 + y 2 x + 3 y = 0 Let z = x + i y Multiplying the second equation with i and adding, we get
z + ∣ z ∣ 2 ( 3 − i ) z ˉ = 3
= > z 2 + − 3 z + ( 3 − i ) = 0
= > z = 2 3 ± 9 − 4 ( 3 − i )
And this gives- x = 2 3 , i y = ± 2 9 − 4 ( 3 − i )
Here I took a leap of faith; without actually calculating y , I assumed that probably in adding all the solutions ( x , y ) they will cancel each other and I will end up adding 3 / 2 twice. Hence the answer is 3. Now, I am a little skeptic as to whether this is just a coincidence. Could someone please help? Thanks in advance.
Moderator note:
Your leap of faith is somewhat incorrect. It just so happens that the ± parts cancel out in the sum of all parts, but it is not true that x = 2 3 , i y = ± 2 9 − 4 ( 3 − i ) . For example, if you were asked for ∑ ( x 2 + y 2 ) , then your approach would not work.
When you set z = 2 3 ± 9 − 4 ( 3 − i ) = x + i y , you needed to equate real and imaginary parts. What we have, is that 9 − 4 ( 3 − i ) = ( 1 + 2 i ) , and so we have z = 2 3 ± ( 1 + 2 i ) = 2 + i , 1 − i .
(2,1) and (1,-1) satisfies the above pair of equation . Put x=åcos(m) y=åsin(m) After solving both equations in a and m we get å^2=2 or 5 (real values) now we plugin the value of a and get m.
And ordered pair as {(1,1),(1,-1),(-1,1),(-1,-1)} for å^2 as 2 and
{(2,1)(2,-1),(-2,1)(-2,-1)} for å^2=5.
Now check which solutions are added because of squaring while solving for å by putting the values.
why don't you use l a t e x it will make the things beautiful
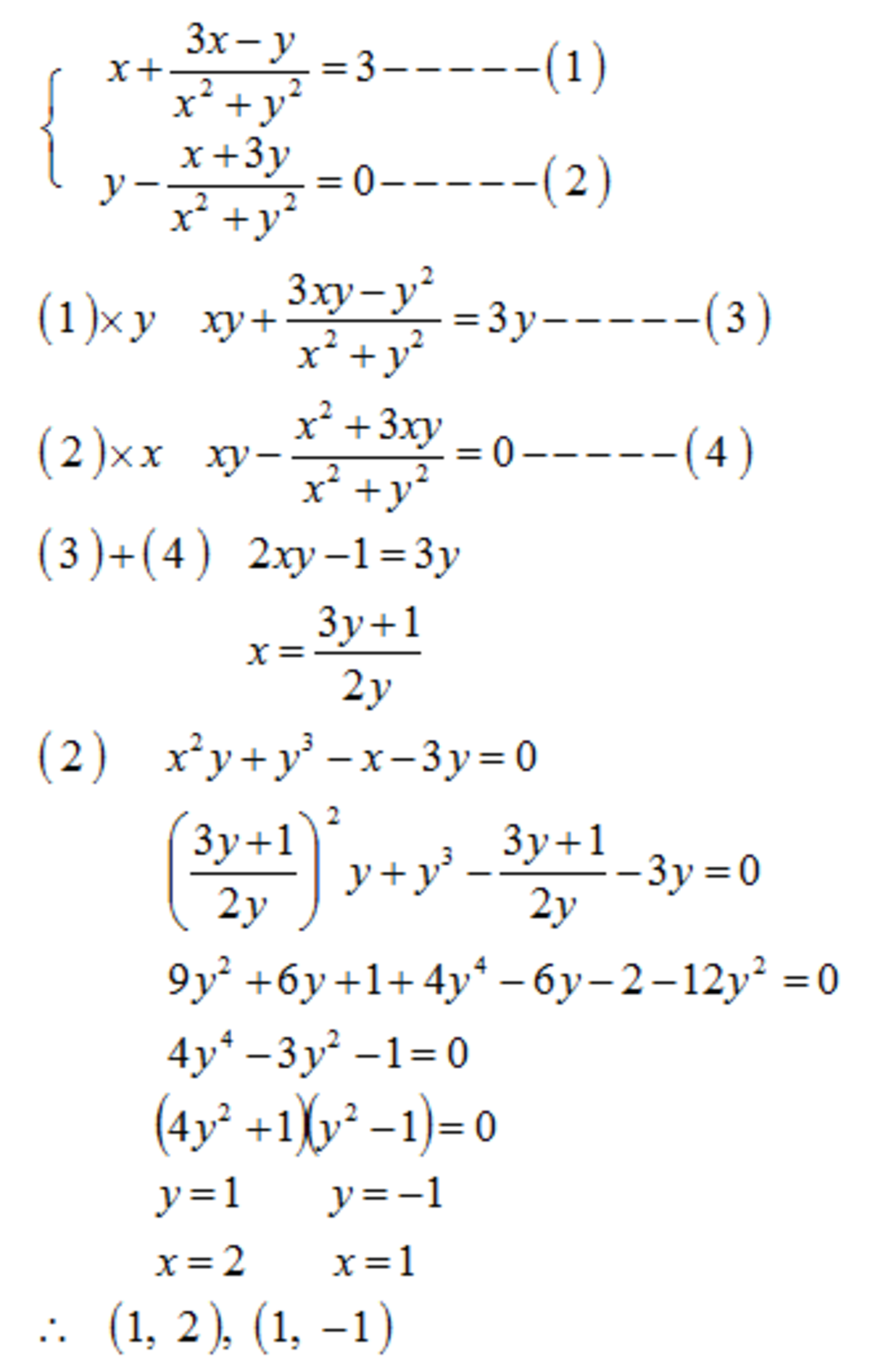
Let z = x + i y . We have z ∗ = x − i y , i z ∗ = y + i x , z z ∗ = x 2 + y 2 .
Then, 3 + 0 i = x + i y + x 2 + y 2 3 x − 3 y i − y − x i = z + z z ∗ 3 z ∗ − i z ∗ = z + z 3 − i .
Clearly, z = 0 is not a solution, so we can multiply throughout by z to obtain z 2 − ( 3 ) z + ( 3 − i ) = 0 .
Factoring this, we get [ z − ( 1 − i ) ] [ z − ( 2 + i ) ] = 0 .
Thus, the only possible solutions are ( x , y ) = ( 1 , − 1 ) , ( 2 , 1 ) .
We can verify that these are indeed solutions to the original equations.