Most distant

Classical Mechanics Level 4

A particle is projected from the height of 200 meters (with an angle) launch speed is the same for all angles, 50 m/s if "g" is 10 m/s^2, then calculate the angle for which the horizontal displacement is maximum for the particle (round it to the nearest integer).(If your answer is x degrees then write the answer as x)

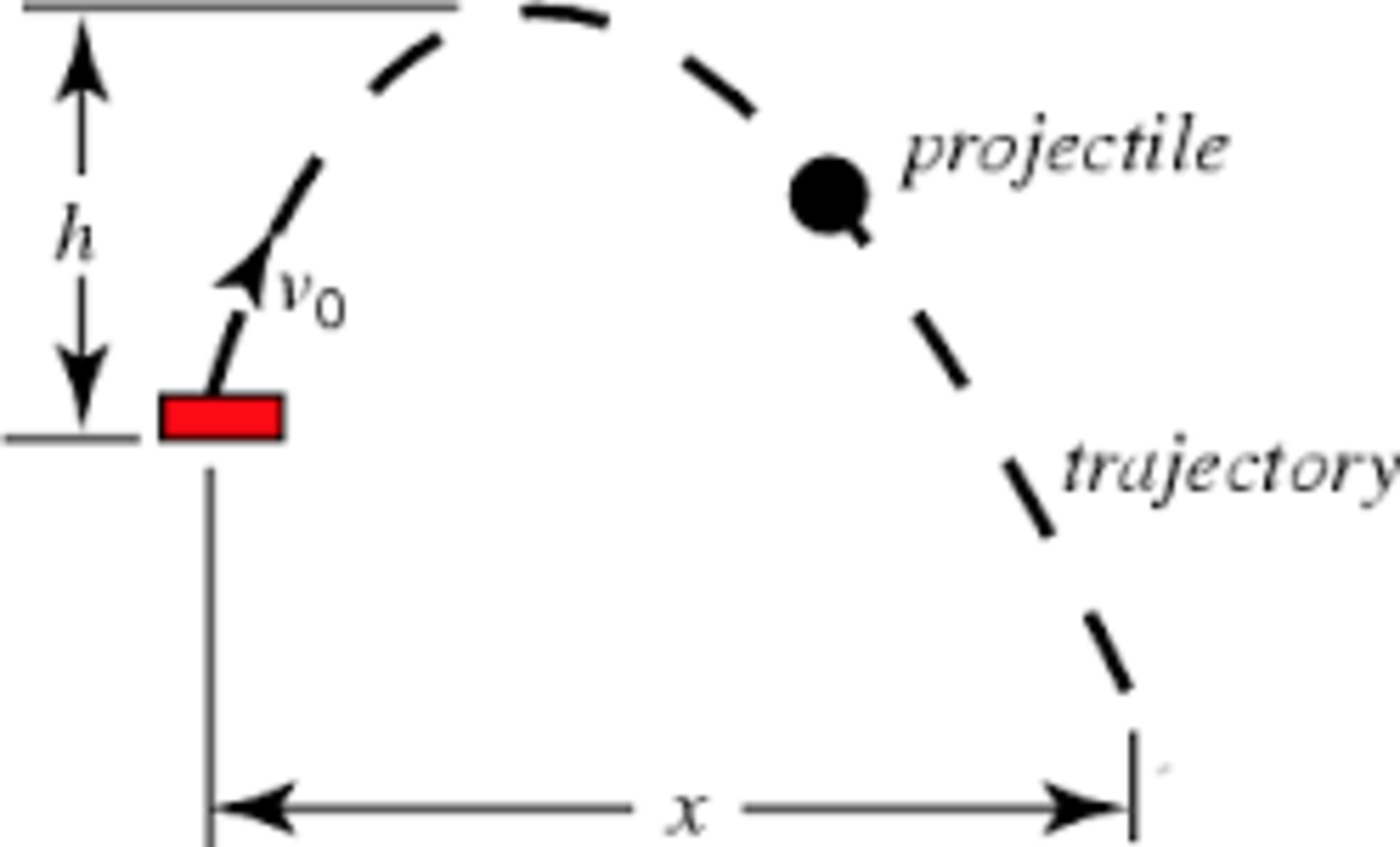
The answer is 32.

1 solution

Krishna Sharma
Apr 3, 2015

Ok, This is going to be short

$\displaystyle sin\theta_{max} = \dfrac{1}{\sqrt{2 + \frac{2gh}{v^2}}}$

Substitute the values to get $\theta_{max} \approx 31.8^{\circ}$

I'll write full solution later because tomorrow in my mains paper :)

Thanx for posting the solution !!!!

Parth Bhardwaj - 6 years, 2 months ago

Please tell how did you get this ?

Rajdeep Dhingra - 6 years, 2 months ago

Most distant

The answer is 32.

1 solution

0 pending reports