Motion on a cone surface
A particle is confined in its motion to the inner surface of a right circular cone whose vertex is at the origin, and opening upward along the positive z axis. Its semi-vertical angle θ c = 3 0 ∘ . The particle initial position is ( 1 0 , 0 , 1 0 3 ) , and its initial velcocity is ( 0 , 1 0 , 0 ) . Find the minimum z coordinate of particle trajectory. Take g = 9 . 8 1 m / s e c 2 . The gravitational acceleration is along the negative z direction.
The answer is 12.283.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath very nice solution. Upvoted
@Karan Chatrath
can you please help me in this problem

You may ask for my attempt.
@Karan Chatrath You may also ask for my attempt. I will happily show you.
Express the coordinates in cylindrical form ( α = 3 ) :
x = r cos θ y = r sin θ z = α r
Lagrangian:
L = 2 1 m ( x ˙ 2 + y ˙ 2 + z ˙ 2 ) − m g z = 2 1 m ( r 2 θ ˙ 2 + r ˙ 2 ( 1 + α 2 ) ) − m g α r
Equations of motion:
d t d ∂ r ˙ ∂ L = ∂ r ∂ L d t d ∂ θ ˙ ∂ L = ∂ θ ∂ L
Evaluating these results in the following expressions for the double-dot terms:
r ¨ = 1 + α 2 r θ ˙ 2 − g α θ ¨ = − r 2 r ˙ θ ˙
Initial conditions:
r = 1 0 θ = 0 r ˙ = 0 θ ˙ = 1
Running a numerical simulation results in z m i n ≈ 1 2 . 2 8 3 . Some plots of the trajectory are included below (up until 100 seconds), along with simulation code.
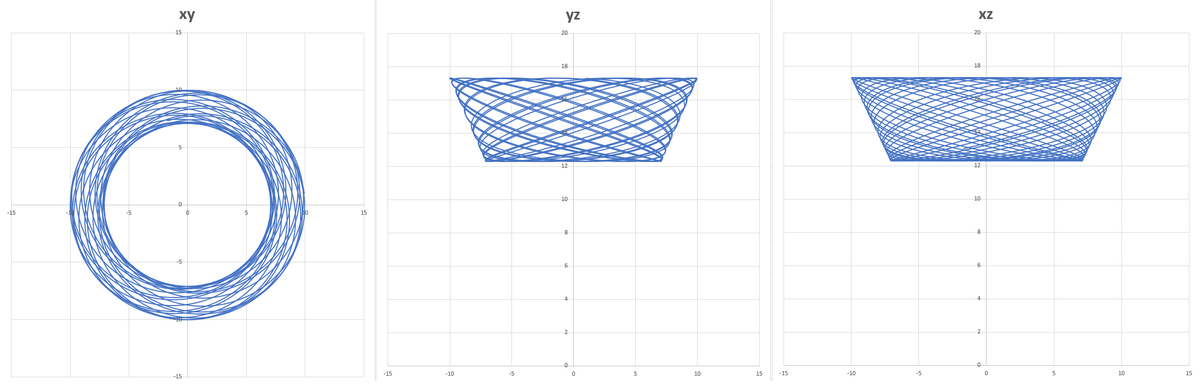
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
|
@Steven Chase very nice solution. Upvoted
An alternate solution to that provided by @Steven Chase . One may refer to his solution for the derivation of energy expressions. Consider the expressions for kinetic and potential energy derived by him. Using that and plugging in α = 3 one gets:
T = 2 m r ˙ 2 + 2 m r 2 θ ˙ 2 V = 3 m g r
r ( 0 ) = 1 0 ; θ ( 0 ) = r ˙ ( 0 ) = 0 ; θ ˙ ( 0 ) = 1
Using the Lagrange's equation with respect to θ , one can easily prove that:
r 2 θ ˙ = 1 0 0
The reader is requested to prove the above by him/her self.
Plugging the above expression in T gives:
T = 2 m r ˙ 2 + r 2 5 0 0 0 m
Applying conservation of energy gives:
T + V = T i n i t i a l + V i n i t i a l
Simplifying by plugging in initial conditions and solving for r ˙ 2 gives:
2 r ˙ 2 = r 2 ( 5 0 + 1 0 g 3 ) r 2 − 3 g r 3 − 5 0 0 0
Now, since:
z = 3 r
THe minimum value of z is achieved when z ˙ = 3 r ˙ = 0 , which means r ˙ = 0 . This means that one must find the roots of the numerator of the expression:
2 r ˙ 2 = r 2 ( 5 0 + 1 0 g 3 ) r 2 − 3 g r 3 − 5 0 0 0 ⟹ ( 5 0 + 1 0 g 3 ) r 2 − 3 g r 3 − 5 0 0 0 = 0
Solving using a computer/ Wolfram Alpha gives one of the roots as:
r o ≈ 7 . 0 9 2 z m i n = 3 r o ≈ 1 2 . 2 8 3 6