Motion on frictionless plane
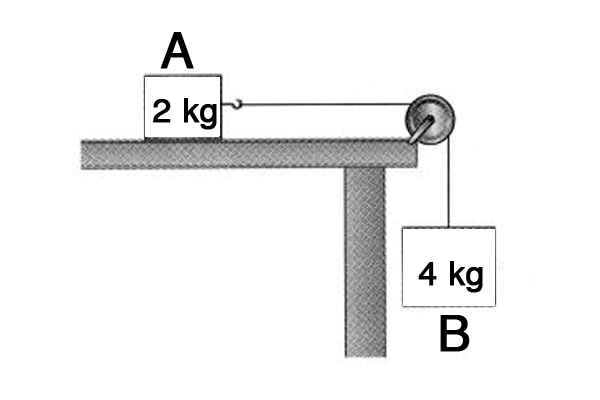 In the above diagram, object
is on a frictionless horizontal plane and is connected to object
by a string and a pulley. What is the tension force on the string when both
and
start to move?
In the above diagram, object
is on a frictionless horizontal plane and is connected to object
by a string and a pulley. What is the tension force on the string when both
and
start to move?
Gravitational acceleration is
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The net force acting on block B with m = 4 Kgs is equal to the gravitational force impeded by the tension force from the string.
We can write it as follows: m B a = m B g − T
We can find the total acceleration of the system by using F = m a again, which is the gravitational force acting on block B divided by the total mass of the system which it is affecting:
m B g = ( m B + m A ) a
By substituting the values in, we get a = 6 4 0 m / s 2
Substituting this value of a into the first equation relating the tension force with the force on object B,
we get T = 3 4 0 N