Rotation + Magnetism = Rotatism
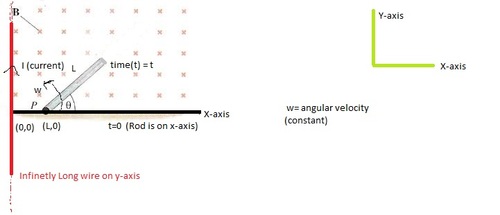 Consider an Thin Conducting Rod of Length L which start's Rotating about an fixed Point P(L,0) in X-Y plane. Initially Rod is on X-axis at an distance of L from origin.(As shown)
Consider an Thin Conducting Rod of Length L which start's Rotating about an fixed Point P(L,0) in X-Y plane. Initially Rod is on X-axis at an distance of L from origin.(As shown)
There is an infinitely long wire on entire Y-axis. And current is flowing Through this wire is I 0
This Rod is rotated By an external agent with Constant angular velocity ω . Then Find the Magnitude of Motional EMF develop between the Point 'P' and centre of the rod at the instant when rod is rotated by an angle θ = 6 0 0
Details and Assumptions
∙ Long wire and Conducting Rod are Placed in X-Y plane.
∙ Rod is Rotated By an external agent so that it can definitely move with constant angular velocity.
∙ EMF means electro motive Force.
Use following data
∙ I 0 = 4 × 1 0 7 A m p . ∙ ω = 4 r a d / s ∙ L = 4 m .
This is Original
This is Part of set mixing of concepts
The answer is 13.7505.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Here I used The Fact the magnetic field due to wire at an distance of x will be B = 2 π x μ 0 I 0 .
And also If an rod of length 'l' moving with velocity 'v' then emf developed in it will be = B l v .
I got the same answer but was marked incorrect. I sent the same as clarification also . It said it accepts only integer answers
I have updated the answer to 13.7505.
Those who previously entered 13 or 14 have been marked correct.
How did you integrate?
Log in to reply
\Ep P 0 = ∫ r = 0 r = L / 2 2 π ( L + r cos θ ) μ 0 I 0 ω r ( d r ) \Ep P 0 = 2 π μ 0 I 0 ω ∫ r = 0 r = L / 2 L + 2 r r ( d r ) ( ∵ cos 6 0 = 1 / 2 ) \Ep P 0 = π μ 0 I 0 ω ∫ r = 0 r = L / 2 2 L + r 2 L + r − 2 L ( d r ) \Ep P 0 = π μ 0 I 0 ω ∫ r = 0 r = L / 2 ( 1 − 2 L + r 2 L ) ( d r ) \Ep P 0 = π μ 0 I 0 ω ( [ r − 2 L + r 2 L ln ( 2 L + r ) ] 0 L / 2 ) \Ep P 0 = 4 π cos θ μ 0 I 0 ω L ( 1 − cos θ 1 ln 1 6 2 5 ) .
Hopes this helps You ! @Tushar Gopalka
Log in to reply
Bro how to integrate!! Hope this is correct dE=uiwxdx/π(2L+x) How to integrate this
General solutions is given by 2 π cos θ μ 0 i ω ( l − cos θ a ( ln ( a a + l cos θ ) ) ) W h e r e : a = D i s t a n c e o f p i v o t f r o m w i r e l = l e n g t h o f r o d θ = a n g l e m a d e b y r o d w i t h h o r i z o n t a l ω = A n g u l a r f r e q u e n c y i = C i r r e n t i n w i r e
I also wrote the exact same integral eqn but I also took the component of the element dx i.e. (dxsin(theta)) And I think we SHOULD take the element or else the integral will be wrong. By the way my answer was coming out to be 11.91( by taking the component of dx)
Let at any Time t=t rod is rotated by an angle ' θ ' So Consider an element of length 'dr' which is at an distance of 'r' from the point of Pivot ( Point P ).
Distance of This element from the wire is
x = L + r cos θ .
Now emf induced between Point P and Centre O is :
\Ep P 0 = ∫ r = 0 r = L / 2 2 π ( L + r cos θ ) μ 0 I 0 ω r ( d r ) \Ep P 0 = 2 π μ 0 I 0 ω ∫ r = 0 r = L / 2 L + 2 r r ( d r ) ( ∵ cos 6 0 = 1 / 2 ) \Ep P 0 = π μ 0 I 0 ω ∫ r = 0 r = L / 2 2 L + r 2 L + r − 2 L ( d r ) \Ep P 0 = π μ 0 I 0 ω ∫ r = 0 r = L / 2 ( 1 − 2 L + r 2 L ) ( d r ) \Ep P 0 = π μ 0 I 0 ω ( [ r − 2 L + r 2 L ln ( 2 L + r ) ] 0 L / 2 ) \Ep P 0 = 4 π cos θ μ 0 I 0 ω L ( 1 − cos θ 1 ln 1 6 2 5 ) .