Mouse and sweets

Probability Level 4

An infinite two-dimensional pattern is indicated below.

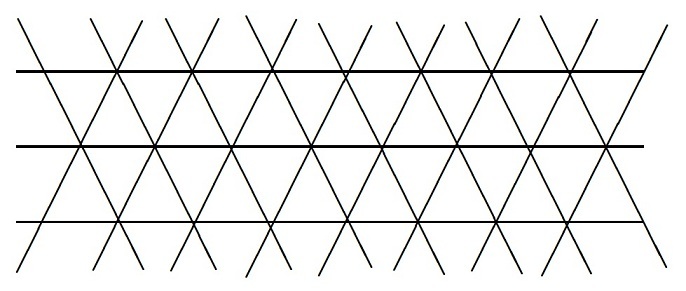
The smallest closed figure made by the lines is called a unit triangle. Within every unit triangle, there is a mouse. At every vertex there is a sweet. What is the average number of sweets per mouse?

3 1 2

\dfrac{1}{2}

\dfrac{1}{3}

2 solutions

Marta Reece
Jun 20, 2017

There are couple of ways to arrive at the answer.

Every mouse is next to 3 sweets, but every sweet is next to 6 mice.

The pattern can be divided into equal sections infinitely repeating.

A small portion of one such possible division is pictured on the left. Each colored section contains two (very round) mice but only one sweet (invisible at the intersection of the lines).

Could you explain method #1 a bit more? I cant see how you can arrive at the answer using just that.

Prateek Saini - 3 years, 11 months ago

You can think of it as having connections between neighbors. Each mouse is inside a triangle and the connections go from it to the three vertices containing the sweets. Having those connections assures us that we are counting "next to" the same way for both mice and sweets. Then we see that each mouse is connected to three sweets, each sweet to six mice. That makes a one to two ratio, so there is one sweet per mouse. If you still don't believe it, you can go for solution #2.

Marta Reece - 3 years, 11 months ago

Prateek Saini
Jul 14, 2017

By joining the center of each triangle we get another infinite grid made up of regular hexagons (shown in picture) each hexagon contains exactly one vertex i.e. one sweet. The area of a hexagon is double the area of a unit triangle. So a very large section of this infinite grid will contain roughly twice as many unit triangles as hexagons (the hexagons in the grid we made) Since each triangle corresponds to mouse and each hexagon corresponds to a sweet, the required fraction is $\dfrac{1}{2}$

Mouse and sweets

2 solutions

0 pending reports