Move the Stack 2
The disks below can be moved from peg to peg according to the following rules:
Only one disk can be moved at a time.
Each move consists of taking the upper disk from a stack and placing it on top of another stack or on an empty peg.
No larger disk may be placed on top of a smaller disk.
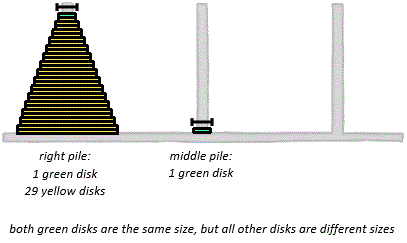
What is the smallest number of moves needed to create a stack of exactly disks in ascending order by size on the middle or right peg?
Inspiration: Move the Stack
The answer is 1610612733.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose we started with 4 disks (in ascending order) with the top two disks the same on one peg and wanted to move the top 2 disks over to another peg. This would take a minimum of 2 moves.
Now suppose we wanted to move the top 3 over to another peg instead. We would need to move the top 2 disks over to one peg ( 2 moves), then move the third disk over to a different peg ( 1 move), and then move the top 2 disks again on top of the third disk ( 2 moves) for a total of 2 + 1 + 2 = 5 moves.
Now suppose we wanted to move the top 4 over to another peg instead. We would need to move the top 3 disks over to one peg ( 5 moves), then move the fourth disk over to a different peg ( 1 move), and then move the top 3 disks again on top of the fourth disk ( 5 moves) for a total of 5 + 1 + 5 = 1 1 moves.
This is a recursive pattern, so that if a n is the minimum number of moves to move n disks (where the top two are the same and the rest are different in ascending order), then a 2 = 2 and a n = 2 a n − 1 + 1 for n > 2 . The first few terms are 2 , 5 , 1 1 , 2 3 , 4 7 , 9 5 , 1 9 1 and so on, and it can be shown by induction to satisfy a n = 3 ⋅ 2 n − 2 − 1 for n ≥ 1 .
In this problem, we are almost moving n = 3 1 disks over, except the first move is already given, and we don't need the last move since we only need to end with a stack of 3 0 , so the minimum number of moves needed is a 3 1 − 1 − 1 = ( 3 ⋅ 2 3 1 − 2 − 1 ) − 1 − 1 = 1 6 1 0 6 1 2 7 3 3 .