Moving Beads About To Collide
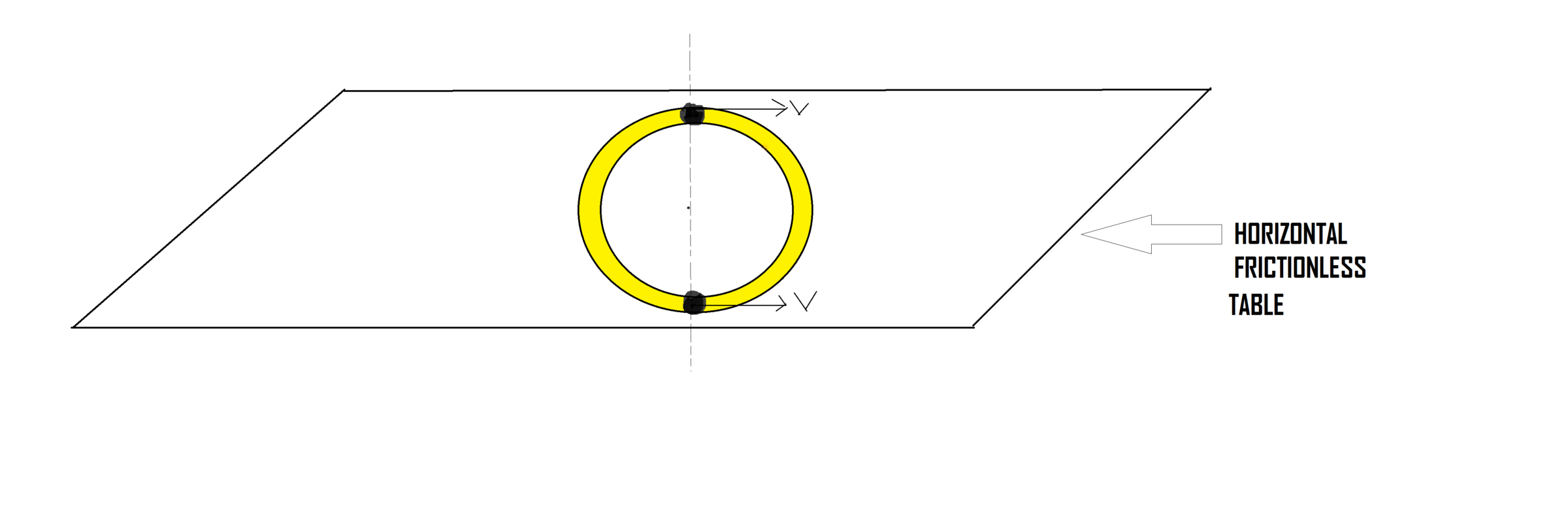
Two identical small beads of mass m kg each are attached to a ring (of mass m kg ), and the total system is kept on a long horizontal frictionless table. Beads are free to move around the ring and there is no friction between the ring and the beads.
Both the beads are given an initial velocity of v m/s and the ring is initially at rest.
Let the magnitude of velocity of the ring at the instant when the two beads are about to collide be x m/s , and let the magnitude of velocity of the lower bead in the diagram be y m/s .
Find the value of ( x y ) 2 .
The answer is 1.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Pick an axis system O x y such that O x is in the direction of the original motion of the beads. By symmetry, both beads will always make the same angle with the x -axis. By symmetry again, the ring will move along the x -axis. Since all reaction forces are smooth, the ring does not rotate.
Suppose that at some time in the motion the centre of the ring has moved a distance u from its starting position, and the two beads make an angle of θ above and below the x -axis. Then the centre of the ring and the two beads have coordinates ( u , 0 ) , ( u + a cos θ , a sin θ ) and ( u + a cos θ , − a sin θ ) respectively. Since all forces acting on the system are either irrelevant (like gravity) or internal, momentum is conserved, and hence m ( u ˙ 0 ) + m ( u ˙ − a sin θ θ ˙ a cos θ θ ˙ ) + m ( u ˙ − a sin θ θ ˙ − a cos θ θ ˙ ) is constant. Thus we deduce that 3 u ˙ − 2 a sin θ θ ˙ is constant. Since, initially, u ˙ = 0 , θ = 2 1 π and θ ˙ = − a v , we deduce that 3 u ˙ − 2 a sin θ θ ˙ = 2 v All forces are conservative, and so energy is also conserved. Thus 2 1 m u ˙ 2 + 2 [ 2 1 m ( u ˙ − a sin θ θ ˙ ) 2 + 2 1 m a 2 cos 2 θ θ ˙ 2 ] is constant, and hence 2 3 u ˙ 2 − 2 a sin θ u ˙ θ ˙ + a 2 θ ˙ 2 = v 2 When θ = 0 , the conservation of momentum equation tells us that u ˙ = 3 2 v , and the conservation of energy equation tells us that a 2 θ ˙ 2 = 3 1 v 2 , and hence a θ ˙ = − 3 1 v . Thus x = 3 2 v , and the velocity of the bead below the x -axis is ( u ˙ − a sin θ θ ˙ − a cos θ θ ˙ ) = ( 3 2 v 3 1 v ) so that y 2 = 9 4 v 2 + 3 1 v 2 = 9 7 v 2 , and hence y = 3 7 v . We deduce that ( x y ) 2 = ( 2 7 ) 2 = 1 . 7 5 If you prefer, we can consider the equation of motion of the bead above the x -axis, which is m ( u ¨ − a sin θ θ ¨ − a cos θ θ ˙ 2 a cos θ θ ¨ − a sin θ θ ˙ 2 ) = − R ( cos θ sin θ ) where R is the magnitude of the reaction of the ring on the bead. This equation reads m u ¨ ( 1 0 ) + m a θ ¨ ( − sin θ cos θ ) + ( R − m a θ ˙ 2 ) ( cos θ sin θ ) = 0 Taking the scalar product of this equation with the vector ( cos θ − sin θ ) , we deduce that − m sin θ u ¨ + m a θ ¨ = 0 , and hence sin θ u ¨ = a θ ¨ If we combine this identity with the (derivative of the) conservation of momentum equation, we can derive the differential equation θ ˙ 2 = a 2 ( 3 − 2 sin 2 θ ) v 2 which again tells us that a θ ˙ = − 3 1 v when θ = 0 . We could, if we wished, solve this differential equation to determine how long it takes for the two beads to collide, namely v a 3 E ( 3 2 ) ≈ . 2 . 1 8 4 4 4 v a where E is the complete elliptic integral of the second kind: E ( k ) = ∫ 0 2 1 π 1 − k 2 sin 2 θ d θ
@Mark Hennings , we really liked your comment, and have converted it into a solution.
such maths , much wow .
Sir can you suggest me some resources for clearing my concepts in physics?
Thanks!
Log in to reply
@Mark Hennings sir.
Log in to reply
it's not easy to advise you, since I don't know what level you feel comfortable with.
The textbook we use in my school is "Introducing Mechanics" by Jefferson & Beadsworth, Oxford University Press. This covers most topics up to and including Further Mathematics A Level in the UK.
If you want something more advanced, I cut my teeth on "Properties of Mechanics" by Synge and Griffiths. This is old-school Mechanics, but advanced material. A more modern treatment of Mechanics (using Lagrangians and Hamiltonians) is provided by Goldstein "Classical Mechanics". Both of these books are available as .pdf's online.
The system starts with energy 2 1 m v 2 + 2 1 m v 2 = m v 2 as well as momentum m v + m v = 2 m v .
Now momentum is conserved, and when the beads collide their velocities in the frame of the ring cancel each other out. Therefore, the total momentum at time of collision is due to the ring carrying the balls for a total mass of 3 m . Therefore, its velocity, v ′ , must be 3 2 v .
The kinetic energy of the ring alone is therefore 2 1 m ( 3 2 v ) 2 = 9 2 m v 2 , so the remaining two beads have a total kinetic energy of 9 7 m v 2 . So due to symmetry, each has an energy of 1 8 7 m v 2 = 2 1 m ( v ball ) 2 . So v ball = 3 7 v . So x y = 2 7 , so ( x y ) 2 = 4 7 = 1 . 7 5 .