Moving Blocks
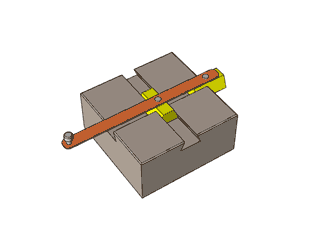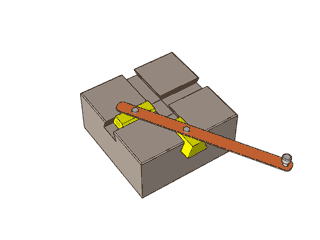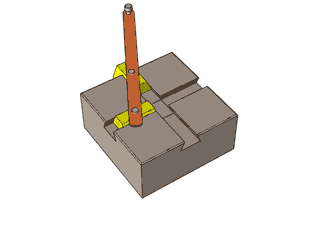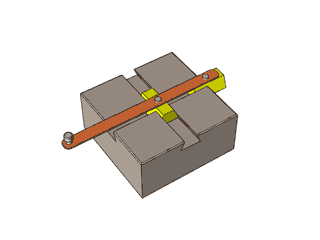 In the figure two blocks are executing simple harmonic motion of same frequency in such a way that when one is at position of maximum displacement then other is at mean position. Now what is the path of external end point of rod.
In the figure two blocks are executing simple harmonic motion of same frequency in such a way that when one is at position of maximum displacement then other is at mean position. Now what is the path of external end point of rod.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions

Or simply attach a long pencil to the moving part and keep the whole setup on a big chart paper
Log in to reply
That's basically what I did in my head. Also, the path was circular so Ellipse and circle where the only options
Log in to reply
Hmm... You can exactly see from the gif , at two sides the stick is more outside and the other two sides comparatively shorter , thus ellipse
 Imgur
Imgur
Even if A and B do not execute SHM, path of P will be the same - an ellipse.
The mechanism is called an Elliptical Trammel. Every point on arm ABP traces an ellipse, with some special cases like the midpoint M of AB tracing a circle (ellipse with equal axes) and points A and B tracing double lines (which are ellipses with one axis of zero length).
Anyway, to find locus of P -
Let θ = angle AB makes with x axis
Then, P x = b cos θ and P y = a sin θ . . . . parametric equation of ellipse
This is called the trammel of Archimedes, but devices that draw conic sections were more likely to be invented during the Roman Era (with the exception of the compass).
Well...I too cud see in the gif...that it was an ellipse.....but its imp to know the concept used!!!
There is no difficulty in solving this just a simple mind work ,creativity ,and. Visualization would suffice to do this.As the rod moves it attains its maximum displacement when one Block comes to mean position and whn the other block comes to mean position it comes near to the block . there are only two possibilities circle or ellipse ...as it is not having a same radius it is ELLIPSE......
You could solve it simply, or you could try to solve it in an unique way and learn.
That is why I applaud Banti Paswan for his solution.
just close the box with something such that you can see only the tip of the rod. You will find it
Symmetrical about x and y with two far and two near. Initially I thought it could be a circle but I felt quite strange that a circle does not seem to be complicated. Then I checked that cardioid is non symmetrical about x and y. If this can draw out a rectangle, then this is too surprising. Only then I noticed the difference of long and short. As an ellipse matches best, I selected ellipse. To be more precise, we must write its equations. I applied a logic of negation instead of confirmation.