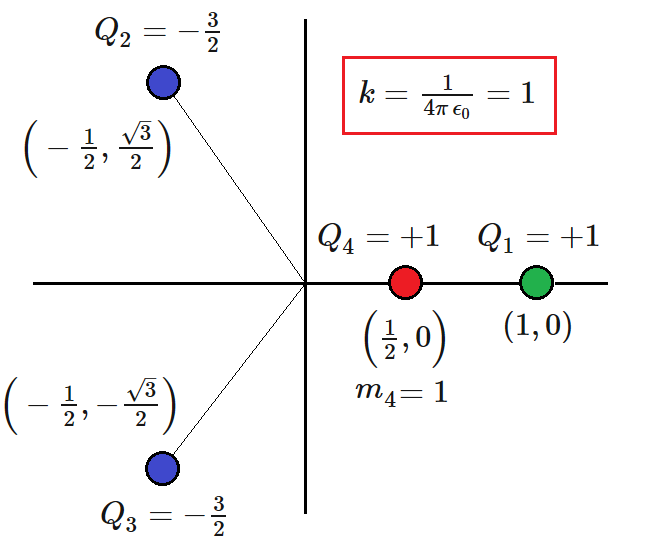
Moving Charge

Let us consider the system of charges. Only $Q_4$ can move freely. Let us consider the charge at its initial position and at the initial instant. The net electrostatic force it experiences at this initial instant is in the negative x - direction. We see there is no net force acting on the charge along the y - direction.

This implies that the motion at all instants of time is confined to be along the X-axis only. This fact can be used to simplify the equations of motion to an extent.

Let us consider the moving charge to be at a general position $(x,0)$ , at a general time t. The potential energy possessed by the charge, due to the other fixed charges, at this instant is:

$V = \frac{1}{\sqrt{(x-1)^2}}-\frac{3}{\sqrt{x^2+x+1}}$

The initial potential energy of the charge is: $V_{initial} = 2-\frac{6\,\sqrt{7}}{7}$

Now, the law of conservation of energy is applied as such. The initial kinetic energy of the particle is $T_{initial}$ .

$T_{initial} + V_{initial} = \frac{\dot{x} ^2}{2} + V$

$T_{initial} = 0$ since the particle is initially at rest.

From here, an expression for $\dot{x}$ is obtained as such:

$\dot{x} = \frac{\sqrt{14}\,\sqrt{21\,\left|x-1\right|-7\,\sqrt{x^2+x+1}-\left|x-1\right|\,\left(6\,\sqrt{7}-14\right)\,\sqrt{x^2+x+1}}}{7\,\sqrt{\left|x-1\right|}\,{\left(x^2+x+1\right)}^{1/4}}$

or: $\dot{x} = F(x)$

Now this expression can be solved by separating the variables and integrating. But before doing so, the limits of integration are to be found. The particle starts from $x = 0.5$ and moves to the left until it reaches $x = -8.493484$ . This number is found by numerically solving $V_{initial} = V$ . Due to the symmetry of the problem, it can be concluded that the particle takes the same amount of time to go from one extreme to the other.

Therefore, the required time is:

$\int_{-8.493484}^{0.5} 2\frac{dx}{F(x)} = T$

This monster is solved numerically. The answer comes out to be: $T = 35.26264 s$

Judging by the expressions, this approach is very tedious. An alternate computational approach can be used as such:

We know the expression for the potential energy of the moving charge. By applying Lagrange's equation, we get $\ddot{x} = -\frac{dV}{dx}$

Knowing the initial conditions, the resulting ODE can be solved using numerical integration. The solution of position of the particle vs. time looks like this: