Moving Chips (Small Input)

Alice and Bob are playing a game called Moving Chips . The game is played on an $n \times m$ board where some cells have some chips on it. Two players move alternately. Each turn consists of one person moving a chip to any cell to its left or any cell to its top. For example, the possible movements of chip A on a $3\times 5$ board are as follows:

The last player who moves all the chips to the top left cell wins.

Consider the configuration below. Alice will move first. Assuming that both players move optimally, who will win the game?

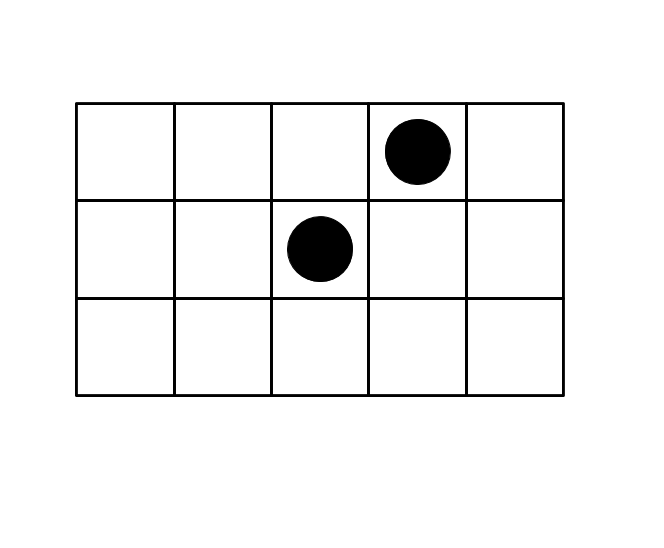
Clarification:

• The chips can be stacked on top of one another.

• The chips can move past any chips.

---

Do you have a generalized strategy for this problem? Then you might enjoy the Large Data version!