Moving Legs of an Equilateral Triangle
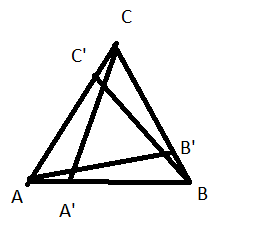 Let
be an equilateral triangle in the plane with side length of
with vertices labeled in counterclockwise order. Let point
coincide with
,
coincide with
, and
coincide with
. Suppose the leg
rotates about
counterclockwise,
rotates about
counterclockwise, and
rotates about
counterclockwise all at the same rate until the three legs intersect at one point. Each leg intersects another leg at a point. These
intersection points trace out paths as the legs rotate. Find the total length of these paths.
Note: The diagram is not completely accurate or to scale.
Let
be an equilateral triangle in the plane with side length of
with vertices labeled in counterclockwise order. Let point
coincide with
,
coincide with
, and
coincide with
. Suppose the leg
rotates about
counterclockwise,
rotates about
counterclockwise, and
rotates about
counterclockwise all at the same rate until the three legs intersect at one point. Each leg intersects another leg at a point. These
intersection points trace out paths as the legs rotate. Find the total length of these paths.
Note: The diagram is not completely accurate or to scale.
The answer is 1.813.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the sides are rotating CCW (Counter Clock Wise) at the same rate, the angle they make at the point of intersection (120°) does not change. This is akin to an angle subtended by a chord (the side of the triangle here) at the circumference of a circle. Hence the path must be an arc of a circle. The radius of the circle will be sin 6 0 1 / 2 = 0 . 5 7 7 and the path will be a 60° arc of this circle. So three such arcs will have the length 3 × 3 π 0 . 5 7 7 = 1.813799