Moving Screen & Objects!
A thin biconvex lens of focal length f = 2 5 cm forms a real image of an object on a screen. The object is separated by 5 cm from the lens. The screen is drawn closer to the lens by a distance of 1 8 cm . Through what distance must the object be shifted so that the image is again formed one the screen?
Give your answers in mm .
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
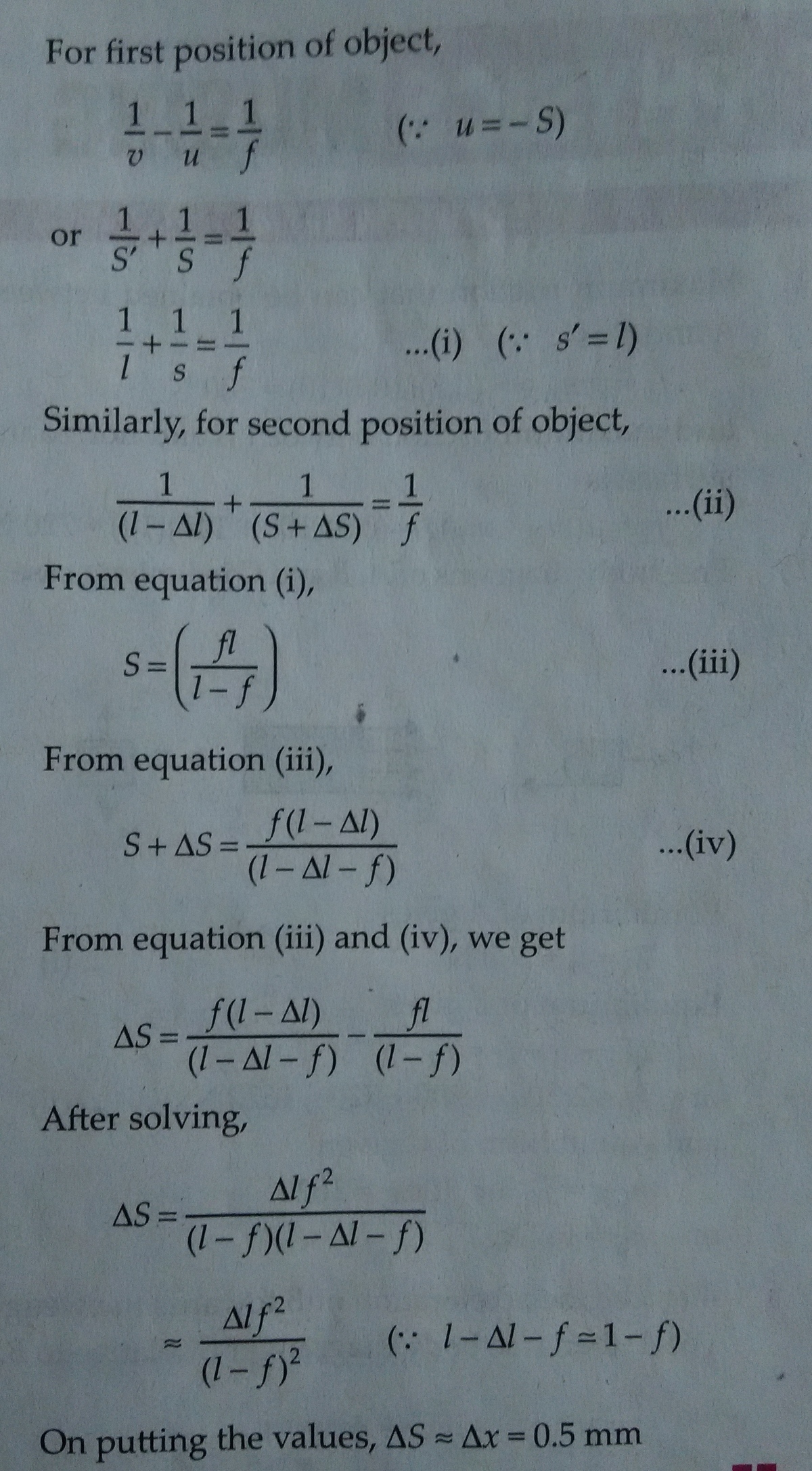

Sir, I have two questions.
1st Question :- In Bangladesh we are taught the equation, (1/u)+(1/v)=(1/f). We put positive sign for REAL Image & negative sign for Unreal Image. Is this wrong? Because, this isn't matching with your equation. Here, in this case, BOTH the Image & Object distance is REAL. So, we can simply write (1/5)+(1/v)=(1/25). But, if we do This, we get that the image comes out to be UNREAL. Where am I Wrong?
2nd Question :- If we keep an object at LESS Distance than the Focal Length of a Biconvex Lens, the Image should be UNREAL. But, here, even if we have put the object LESS Distance (5 cm) than the Focal Length (25 cm), how can the image be REAL? Maybe, I am wrong. But, please Reply & kindly help me to make my concept clear. I want to know the actual correct knowledge about this Formula & it's application. If possible, kindly provide me some Link or any other source where it is described correctly and more precisely.
Log in to reply
you are getting confused somewhere between ( v 1 − u 1 = f 1 ) (Len's Formula) with the Mirror Formula ( v 1 + u 1 = f 1 )
Log in to reply
Thanks a lot for pointing it out and sharing the idea. Thanks, Nishant.