Mr Ant
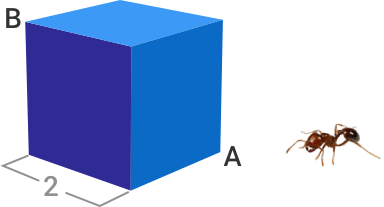
If the solid cube has edge length 2, then what is the shortest distance that an ant can walk from corner A to corner B?
Note : The ant can walk anywhere along the surface of the cube.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
Very Nice Problem, so a beautiful solution for it.
Beautiful!
Doesn't (2+2route2)^2 = 12 though? Making edge then straight in fact the shortest route.
No: ( 2 + 2 2 ) 2 = 2 2 + ( 2 2 ) 2 + 2 ⋅ 2 ⋅ 2 2 = 1 2 + 8 2 ≈ 2 3 . 3 .
Walking through edge then straight is longer. Try it on a cardboard, make a box, you'll see that it's the same with a non-folded cardboard.
"While the cube may be 3D, we're really dealing with a 2D problem..." so yep it's 3D, he just said that the problem is the same with 2D figures.
I thought of the ant making the optimal path shown over the cube's surface in analogy to a "great arc" over a sphere.
Here what you have considered is body diagonal. The formula to find body diagonal of a cube is sqrt(3) *side. Moreover ant cannot travel through body diagonal path as it is empty space (it cannot fly).
The ant could not go inside the SOLID cube. It has no empty space in it. Please read the problem.
3 th solution is the right one. I made the same solution .
My method was purely algebraic. The only logical input is that the ant will want to walk along geodesics for each of the two faces it walks on, since this is guaranteed for 2-D geometry to create the shortest path.
The ant will head for a point somewhere along the edge joining the two faces it traverses. Let's say that the distance along the edge is x . By Pythagoras' theorem, the distance travelled is x 2 + 2 2 .
Now it has to walk a second hypotenuse to get to the point B, with the triangle having legs of 2 c m and ( 2 − x ) cm. By Pythagoras' Theorem again, the distance travelled is 2 2 + ( 2 − x ) 2 .
Let's call the total distance walked by the ant y, where y = x 2 + 2 2 + 2 2 + ( 2 − x ) 2 . We want to minimise y , and we can do this by differentiating y with respect to x to find any stationary points on the function (where d x d y = 0 ).
I used the chain rule with the two parts of the equation separately, then combined them to form the differential equation here: d x d y = x 2 + 4 x + x 2 − 4 x + 8 x − 2 .
Next I solved this equation, where d x d y = 0 :
x 2 + 4 x + x 2 − 4 x + 8 x − 2 = 0
− x 2 + 4 x = x 2 − 4 x + 8 x − 2
x 2 + 4 x 2 = x 2 − 4 x + 8 ( x − 2 ) 2
x 4 − 4 x 3 + 8 x 2 = x 4 + 4 x 2 − 4 x 3 − 1 6 x + 4 x 2 + 1 6
1 6 x = 1 6
x = 1
Putting this back into the equation, y = 2 5
Method 1:-
Divide the back wall into two halves by drawing a line vertically. Then the length of the diagnol of the rectangle with edge A = a 2 + ( 2 a ) 2 = 4 5 a 2 .
Name the edge opposite to A in the rectangle as C. Now, divide the upper wall into two rectanglesby drawing a line from C. Calculate the diagnol of the rectangle with edge B = a 2 + ( 2 a ) 2 = 4 5 a 2 .
∴
The shortest distance travelled =
2
×
4
5
a
2
=
5
a
=
2
.
2
3
6
a
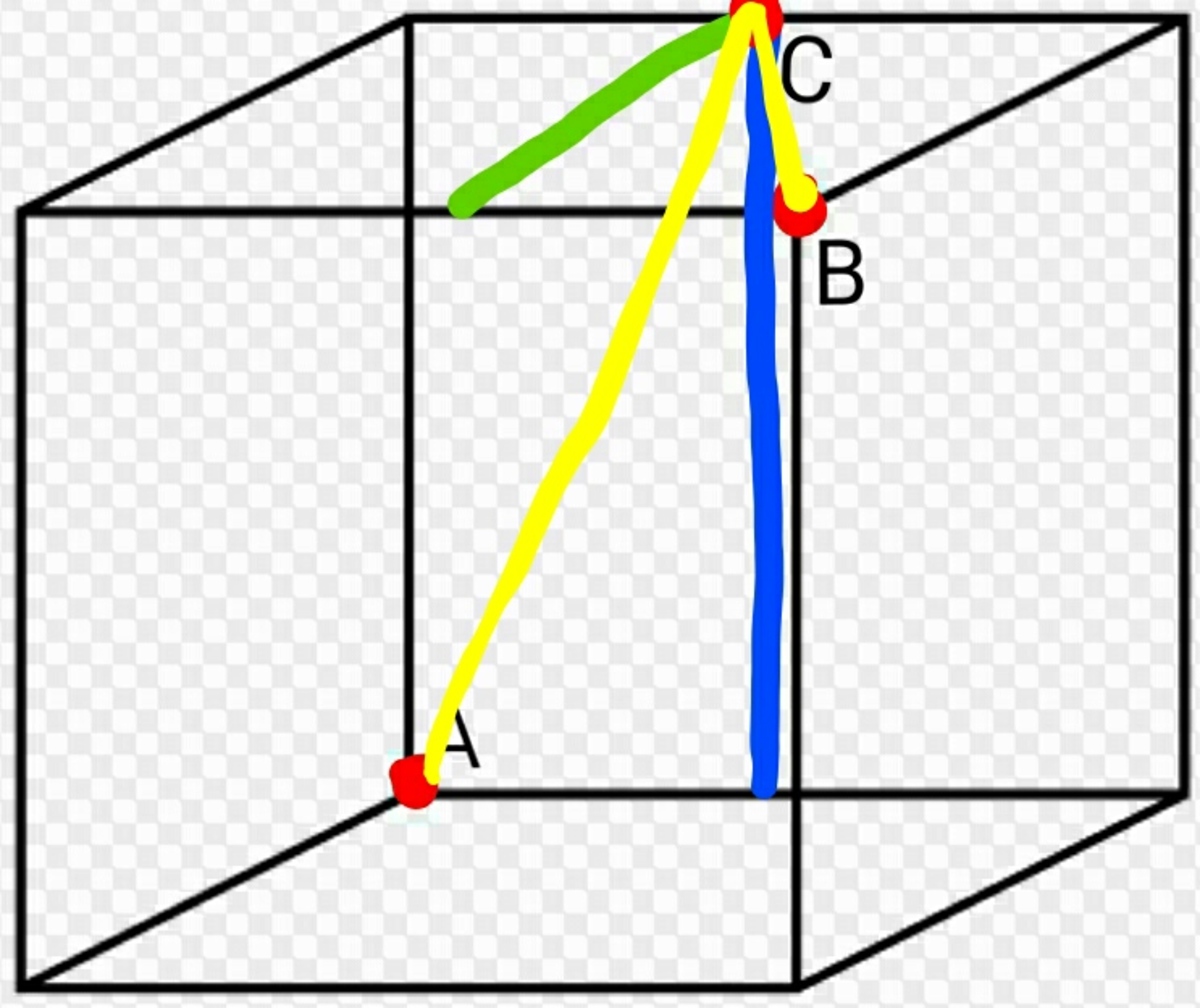 The ant travels along the yellow line
0
The ant travels along the yellow line
0
Let Point
C
be
a
n
y
point
2
units away from point
A
.(
2
units means that
C
is a vertex of the cube). Let Point
D
be the point
2
units away from point
B
and not coplanar (on the cube) with
C
. From these points, we can form a rectangle
A
C
B
D
with side lengths
2
and
4
(
2
×
2
)
. The shortest distance of this rectangle is the diagonal, which must be the shortest distance an ant can travel.
Using Pythagorean Theorem we can solve for the length of the diagonal, that is:
a
2
+
b
2
=
p
2
p
=
a
2
+
b
2
where
a
and
b
are the sides of the rectangle.
Since this distance is squared
p
2
we can square the diagonal,
Thus,
(
a
2
+
b
2
)
2
=
p
2
=
a
2
+
b
2
=
p
2
plugging sides
2
and
4
as either
a
or
b
, we have:
(
2
)
2
+
(
4
)
2
=
p
2
p
2
=
4
+
1
6
p
2
=
2
0
p
=
2
0
.
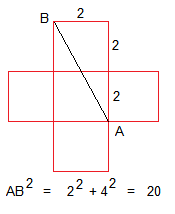
Relevant wiki: Pythagorean Theorem
At first, we might think it is most efficient to walk along the edges of the cube. This would require walking along three edges, for a total distance of 6:
However, it then becomes clear that once we get to the top face of the cube, we'd rather walk straight to point B, for a total distance of 2 + 2 2 :
But wait! What we really want to do is walk "straight" to point B for the entire trip. We want the ants path to look something like:
While the cube may be 3D, we're really dealing with a 2D problem, since the ant can only walk along the surface of the cube. To find the optimal path, we can imagine "flattening" the surface of the cube:
Thus, the shortest path is the hypotenuse of a right triangle with legs of length 2 and 4 , so via the Pythagorean Theorem , the shortest distance is 2 2 + 4 2 = 2 0 .