Mr. X: Is this Geometry of Classical Mechanics?
Mr. X is in a palace of an evil villain. He is equipped with a fully-loaded special type of pistol which has four bullets in one chamber. The muzzle velocity of the gun is . He walks up the steps shouting out his name. Mr. X looks in one direction and sees a man rushing towards him. He lifts his gun and fires, disarming him. However he receives a blow on the head from behind and falls down the stairs.
When Mr. X looks up, he sees the villain pointing the gun on his face. The villain says, "You are the sole cause of my fall from grace Mr. X. It's time for you to say goodbye to this world". The villain pulls down the hammer of the gun.
Mr. X thinks that all is lost, but realizes that if he knows the exact momentum of the bullet, he can stop it in time by using his special powers. He remembers that the radius of the chamber is .
The bullet is in a form of a cylinder of height mounted upon a hemisphere. The cylinder is made up of lead and the hemisphere of antimony.
What will be the momentum of the bullet in ?
Details and Assumptions
-
The radius of the bullet can be found with the help of the size of the chamber. Also the cylinder and hemisphere have the same radius.
-
The density of lead is and that of antimony is .
-
The momentum can be calculated using the mass of the bullet and muzzle velocity of the gun.
-
Give the answer correct to 3 decimal places.
-
Given Below is the diagram of the chamber and the bullet.
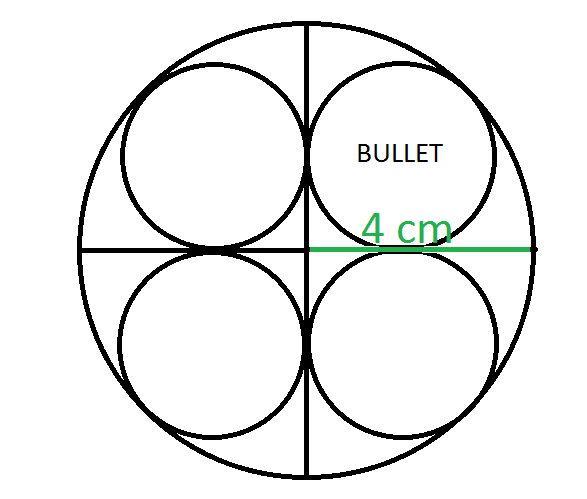
1711533.png)
The answer is 35.721.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The two points where the circle tangentially touches the quadrant's sides is of the same distance. ( x + r ) 2 = r 2 + r 2
x + r = 2 r .
Therefore Radius of Bullet = 1 + 2 (Radius of Chamber) .
= 1 + 2 4 .
= 1 . 6 5 6 8 5 4 2 4 9 4 9 cm .
Now we need to find the volume and mass of the Cylinder.
Radius = 1.65685424949 cm.
Height = 3 cm.
Volume = π ∗ r 2 ∗ h = π ∗ 1 . 6 5 6 8 5 4 2 4 9 4 9 ∗ 1 . 6 5 6 8 5 4 2 4 9 4 9 ∗ 3 = 25.8725800537 \text{cm^{3}} .
The cylinder is made up of lead.
Density = ( V o l u m e ) ( M a s s ) .
Density of Lead = 1 1 . 3 4 g cm − 3
Therefore Mass = Volume*Density = 1 1 . 3 4 ∗ 2 5 . 8 7 2 5 8 0 0 5 3 7 g .
= 293.395057808 g.
Now we need to find the volume and mass of the Hemisphere..
Radius = 1.65685424949 cm.
Volume = 3 2 ∗ p i ∗ r 3 = \pi*0.66667*1.65685424949*1.65685424949*1.65685424949) = \(9.52602093493 \text{cm^{3}} .
The hemisphere is made up of antimony.
Density of Antimony = 6.70 g cm − 3
Therefore Mass = 6 . 7 ∗ 9 . 5 2 6 0 2 0 9 3 4 9 3 g .
= 63.824340264 g.
Now we add them up to find the total mass of the bullet.
= 293.395057808 g + 63.824340264 g = 357.219398072 g.
Now we need to find the momentum of the body.
Momentum = M a s s × V e l o c i t y .
Momentum = 1 0 0 0 3 5 7 . 2 1 9 3 9 8 0 7 2 k g × 1 0 0 ms − 1 .
Momentum of the bullet is 3 5 . 7 2 1 kg ms − 1 .
Mr. X stops the bullet successfully much to the amazement of the villain. \