Multi Inductor/Conductor Circuit

Electricity and Magnetism Level 4

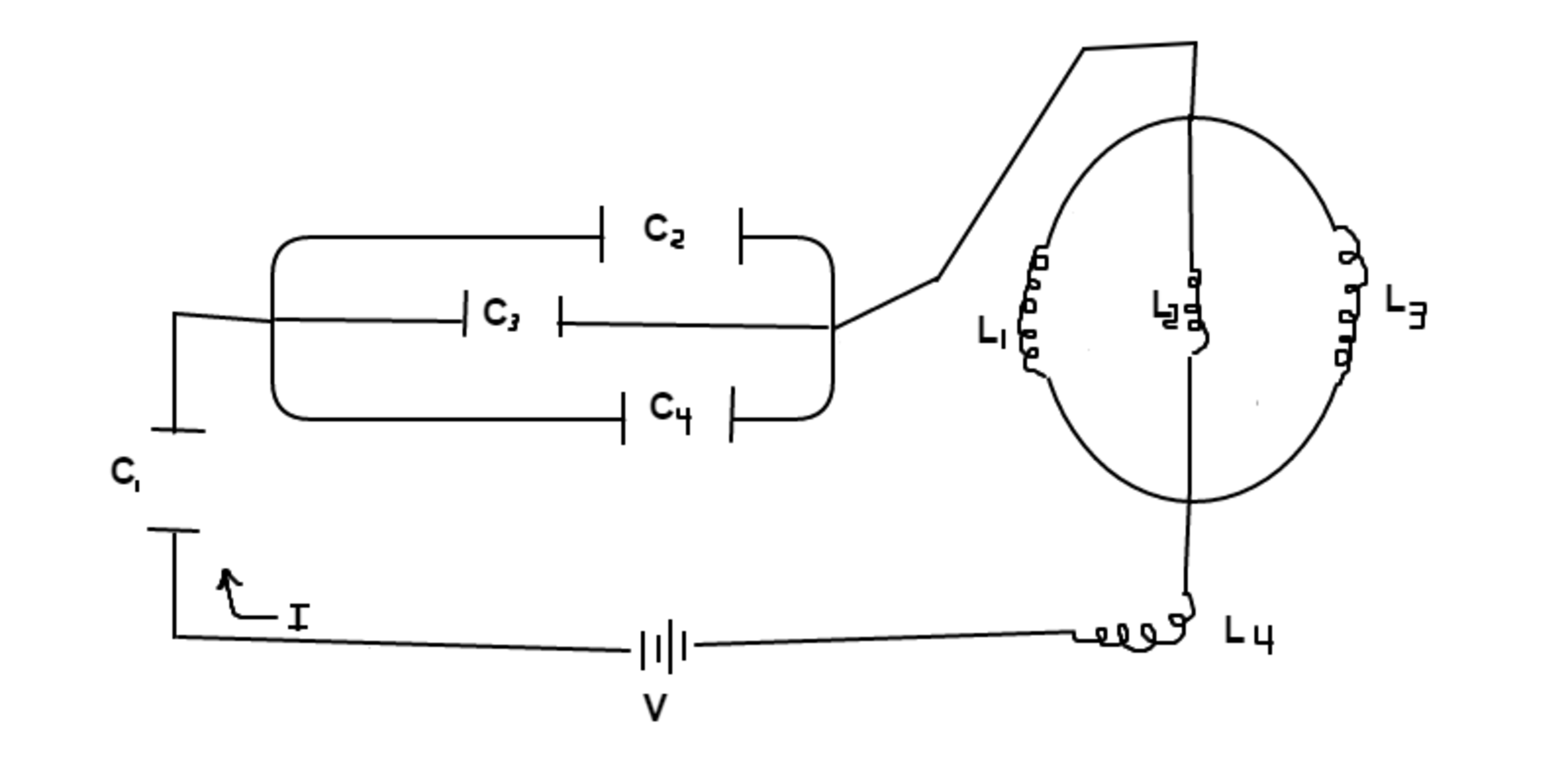
The image above depicts an LC circuit consisting of four inductors ( $L$ ) and four capacitors ( $C$ ). The conductors have the following conductance values: $C_1=20F$ , $C_2=5F$ , $C_3=7F$ , and $C_4=8F$ . The inductances of the inductors are as follows: $L_1=9H$ , $L_2=12H$ , $L_3=18H$ , and $L_4=6H$ . Determine the angular frequency ( $\omega$ ) of the circuit in radians per second.

Note : $\omega = \dfrac{1}{\sqrt{LC}}$ .

David's Electricity Set

The answer is 0.1.

1 solution

David Hontz
May 26, 2016

$C_{2,3,4}=C_2+C_3+C_4=5+7+8=20F \\ \frac{1}{C_{circuit}}= \frac{1}{C_1}+\frac{1}{C_{2,3,4}}=\frac{1}{20}+\frac{1}{20} = \frac{1}{10} \Rightarrow \boxed{C_{circuit}=10F}$ $\frac{1}{L_{1,2,3}}= \frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}=\frac{1}{9}+\frac{1}{12}+\frac{1}{18}=\frac{1}{4} \Rightarrow L_{1,2,3}=4H \\ L_{circuit}=L_4+L_{1,2,3}=6+4=\boxed{L_{circuit}=10H}$ $\omega=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{10 \times 10}}=\frac{1}{\sqrt{100}}=\frac{1}{10}=\boxed{\omega =0.1 rad/s}$

Multi Inductor/Conductor Circuit

David's Electricity Set

The answer is 0.1.

1 solution

0 pending reports