Multi Inductor/Resistor Circuit

Electricity and Magnetism Level 3

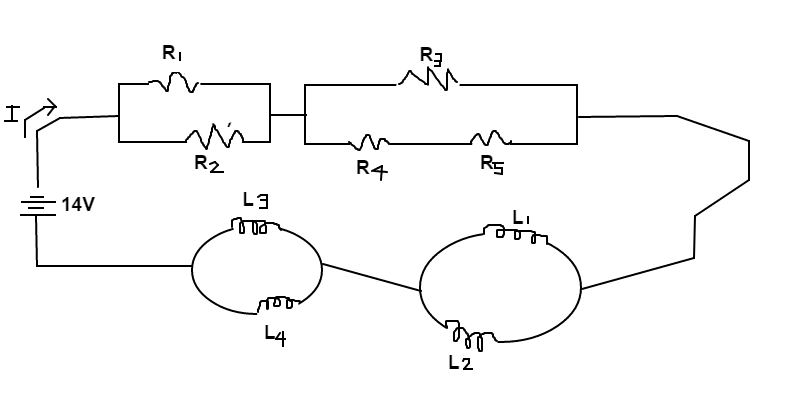
In order to prepare an LR circuit, you arrange a $14V$ battery with five resistors ( $R$ ) and four inductors ( $L$ ), as shown above. The resistors in this circuit have the following resistances: $R_1=6Ω$ , $R_2=12Ω$ , $R_3=12Ω$ , $R_4=5Ω$ , and $R_5=7Ω$ . The inductances of the inductors are as follows: $L_1=18H$ , $L_2=9H$ , $L_3=6H$ , and $L_4=3H$ . Determine the time constant ( $\tau$ ) of this LR circuit in seconds.

Note: $\tau=\frac{L_{circuit}}{R_{circuit}}$

David's Electricity Set

The answer is 0.8.

1 solution

David Hontz
May 26, 2016

In simplifying resistors and inductors, the math depends on whether they are in parallel or in series. $R_{4,5} = R_4+R_5=5+7 = 12Ω \\ \frac{1}{R_{3,4,5}} = \frac{1}{R_3} + \frac{1}{R_{4,5}} = \frac{1}{12}+\frac{1}{12} = \frac{1}{6} \Rightarrow R_{3,4,5}=6Ω \\ \frac{1}{R_{1,2}} = \frac{1}{R_1} + \frac{1}{R_2} = \frac{1}{6}+\frac{1}{12} = \frac{1}{4} \Rightarrow R_{1,2}=4Ω \\ R_{circuit} = R_{1,2}+R_{3,4,5} = 4+6= \boxed{10Ω}$

$\frac{1}{L_{1,2}}=\frac{1}{L_1}+\frac{1}{L_2}=\frac{1}{18}+\frac{1}{9} =\frac{1}{6} \Rightarrow L_{1,2}=6H \\ \frac{1}{L_{3,4}}= \frac{1}{L_3}+\frac{1}{L_4}=\frac{1}{6}+\frac{1}{3} =\frac{1}{2} \Rightarrow L_{3,4}=2H \\ L_{circuit}=L_{1,2}+L_{3,4}=6+2=\boxed{8H}$

$\tau = \frac{L_{circuit}}{R_{circuit}}=\frac{8H}{10Ω} = \boxed{0.8s}$

Multi Inductor/Resistor Circuit

David's Electricity Set

The answer is 0.8.

1 solution

0 pending reports