Multi-Segment Torque
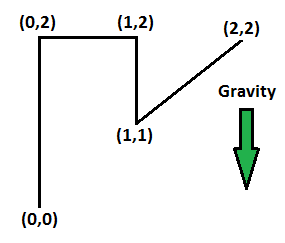
A bent wire has a mass which is uniformly distributed over its length. There is a uniform downward gravitational acceleration .
The coordinates of the end points and bend points are illustrated above.
If the torque about point can be expressed as , determine the value of (to 3 decimal places).
Note: Neglect units and assume that all physical expressions take their simplest forms
The answer is 0.669.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Note that the segment from (0,0) to (0,2) does not contribute to the moment about (0,0) as the perpendicular distance of the line of action of the weight of the entire segment from the axis of the pivot is 0. Thus, we only calculate the moment contributed by the other segments.
There are a total of 3 segments we need to consider, of 1, 1 and s q r t 2 units. The segments of length 1 unit are of mass 4 + s q r t 2 s q r t 2 M each and the segment of length {sqrt{2}} units is of 4 + s q r t 2 s q r t 2 M.
Having calculated the masses, we now need to compute the respective perpendicular distances from the axis of the pivot (x=0).
For the segment closest to the pivot, we sum up the perpendicular distances of each individual point from the axis of the pivot by integrating the function y = x from x=0 to x=1, with respect to x. We get a total perpendicular distance of 0.5 units.
For the segment next closest to the pivot, we again sum up the distances but this time, by taking the area of the square of unit length formed by the line segment with the y-axis. We get a total perpendicular distance of 1 unit.
For the last segment, we sum up the distances by integrating the function y = x from x=1 to x=2, with respect to x. We get a total perpendicular distance of 1.5 units.
Therefore, the total moment about (0,0) caused by gravitational acceleration is
( 1 . 5 × 4 + 2 2 + 1 . 5 × 4 + 2 2 ) M g = 0 . 6 6 9 M g (to 3 d.p.)