Multicolored staircase
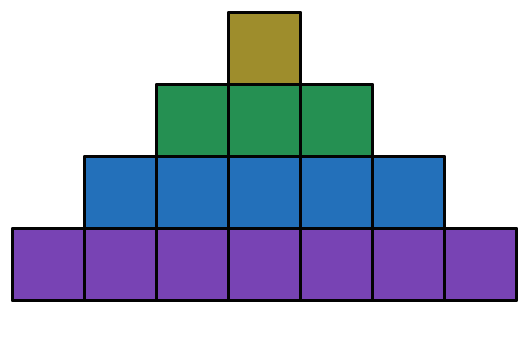 How many ways are there to pick 2 (unit) squares of different colors?
How many ways are there to pick 2 (unit) squares of different colors?
Can you generalize to many rows?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Nice approach of using the complement, which makes is slightly easier.
Let us start from the top.
Since there is only one yellow square, number of ways yellow square can appear in the selected two squares= 15(one yellow square & taking any one square from the rest 15)
We have now considered all possibilities of yellow square, so no need to consider it anymore.
Number of ways we can select 2 squares with one being green= 3*12
Number of ways we can select 2 squares with one being blue= 5*7
So total number of ways to select the required two squares =15+36+35=86
1 (4^2-1^2) + 3 (4^2-2^2) + 5 (4^2-3^2) + 7 (4^2-4^2) = 15 + 36 + 35 = 86
Hm, can you explain what you are doing, and why it works? I don't quite understand what 3 × ( 4 2 − 2 2 ) is meant to refer to.
Log in to reply
When we have sequence of odd numbers, we can say the sum of one to 'n'th term becomes n^2 for example, 1 = 1^2, 1 + 3 = 4 = 2^2, 1 + 3 + 5 = 9 = 3^2 etc... Therefore available combination for first square is(4^2-1^2) , and available combination for second line is (4^2-2^2), and we have 3 squares in second line, so all possibility is 3(4^2-2^2), and so far and so on.
looks complicated, but procedure is not really hard to understand.
00 35 21 07
35 00 15 05
21 15 00 03
07 05 03 00
Addding rows or columns and dividing by 2
(63 +55 + 39+15 )/2 =86
Any idea what the general form is like?
Log in to reply
Have revised my initial answer to show my process. I envision that one could use the same process no matter the size of the stair case, though it would deteriorate of course if there is no upper bound.
I assume that N is an Positive odd number ... summation of ( ((n -2) +1)^2 /4) n {the sum of odd below n * n} = ((n-1)^2/4) n where n form 1 to N by step 2 .
Here's an iterative approach. The key is combine blocks of different colours systematically, going over all pairs and never repeating yourself.
Take row one and all its blocks, in this case it's one block. Combine them with all blocks on next row. There's only 3 possible pairs between them.
Next, combine block on row one with all blocks on the row below. That makes 5 possible pairs.
Same for the last block for 7 pairs.
We have now exhausted all possible pairs of block from row 1 with any other block in the ladder, and we've calculated their number: 1 ∗ 3 + 1 ∗ 5 + 1 ∗ 7
Likewise, we now focus on blocks from row 2 and start combining them with blocks on rows below. Similar to our earlier procedure, we calculate 3 ∗ 5 + 3 ∗ 7 .
Same procedure for row 3 yields 5 ∗ 7
Adding it all up we get 1 ∗ 3 + 1 ∗ 5 + 1 ∗ 7 + 3 ∗ 5 + 3 ∗ 7 + 5 ∗ 7 = 1 5 + 1 5 + 2 1 + 3 5 = 8 6 .
More generally: ∑ i = 1 n ∑ j = i + 1 n ( 2 i − 1 ) ( 2 j − 1 ) , where n > 1 is number of rows.
To construct this expression we can group sums for the ladder:
- 1 ∗ 3 + 1 ∗ 5 + 1 ∗ 7
- 3 ∗ 5 + 3 ∗ 7
- 5 ∗ 7
There's two kinds of multiplicands on each row: ones that change are ones that stay the same. We can rewrite those that change with a well known expression for writing down odd numbers: ( 2 k − 1 ) , where k = 2...n.
- 1 ∗ ( 2 ∗ 2 − 1 ) + 1 ∗ ( 2 ∗ 3 − 1 ) + 1 ∗ ( 2 ∗ 4 − 1 )
- 3 ∗ ( 2 ∗ 3 − 1 ) + 3 ∗ ( 2 ∗ 4 − 1 )
- 5 ∗ ( 2 ∗ 4 − 1 )
We can rewrite these expressions in notation for sums:
- ∑ j = 2 n 1 ∗ ( 2 j − 1 )
- ∑ j = 3 n 3 ∗ ( 2 j − 1 )
- ∑ j = 4 n 5 ∗ ( 2 j − 1 )
Last step: generalize the multiplicand to the left of the * sign. Since it's an odd number changing from sum to sum, we can try using 2 k − 1 again, by making k dependent on summation index: ∑ i = 1 n ∑ j = i + 1 n ( 2 i − 1 ) ( 2 j − 1 )
Orange color= O=1, green=G=3, blue=B=5 purple=P=7.
O appears 15 times, G appears 35 times.
3 * 5+3 * 7=36, B= 35=5 * 7.
O+G+B=15+36+35=86

Its simple, ways of selecting 2 blocks is 16c2 we have 2 subtract ways if selecting 2 similar blocks i. e. 7c2 + 5c2 + 3c2 hence we got the answer as 120-21-10-3=86