Multiple Balls Bouncing
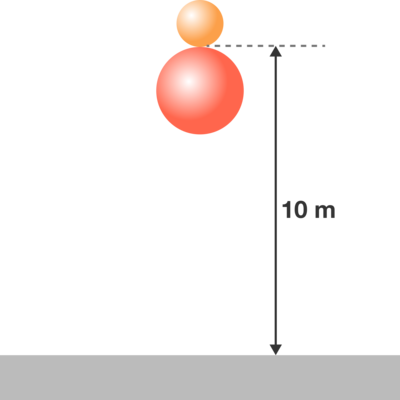
A small ball is placed on top of a bigger, heavier ball at a height of 1 0 m above the ground.
When the balls are simultaneously released and bounce, how high will the smaller ball bounce up to?
Assumptions:
- All collisions are perfectly elastic, which means no kinetic energy is lost in the collisions.
- Air resistance is negligible.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
uhhhhhh.... ????????????????/
Log in to reply
It's an video made by Physics Girl explaining the physics of the stacked ball drop.
great vid!
The bigger ball transfers some of its momentum to the smaller ball. Since mass of the bigger ball is more than the mass of smaller ball, momentum produced due to velocity of the bigger ball will result in more velocity in the smaller ball. ( When momentum is constant, mass is inversely proportional to velocity.)
What you said is really wonderful
When put in normal conditions a ball that has been dropped would gather up kinetic energy on the way down and when it hits the ground it will lose some of it's energy to the ground in order to bounce back up and complete it's given task. However, no matter how many times the ball bounces it will never be able to reach it's original height of drop or to put it another way, it will never have enough energy to get back up to where it started, hence the law of conservation of energy.
But now since a smaller ball, let's call it ball b , is placed on top of the larger or normal sized ball, let's call that ball a , the energy that will be given at the point of impact to the ground, will not only be to the ground but to the ball b on top of it as well. When the larger ball hits the ground it doesn't just bounce back up like a sheet of metal, but instead it stretches and pushes itself upwards due to the amount of elasticity in it's material. And when this stretching happens in normal conditions, the ball only touches the air molecules around it, which are so small that they have a negligible affect on the ball's performance and it bounces nearer to the original drop point.
But in the case with ball b , the ball a has another surface on which it can transfer most of it's remaining elastic energy, or in other words, it's jumping power. Since the ball b has a lot less area than the ball a for air resistance to slow it down, ball b actually goes much higher than the point of drop due to it's lack of area, mass and volume to keep it below the drop point. Also the fact that it now has the energy of an object 3x it's size, so that's another, shorter, reason why it goes off shooting into space.
Many flaws: - no energy is given to the ground; - power is not energy; - air resistance has nothing to do with it.
Log in to reply
If the ground is elastic then strain energy is given to the ground. Consider a single ball impacting the ground, as the ball’s velocity is instantaneously zero all the kinetic energy in the ball is transformed to strain energy in both the ball and the floor (think of a trampoline bed).
Log in to reply
It is correct that IRL the ground will temporarily take some potential energy. If we consider the ground to be infinitely stiff however, then this energy exchange gets reduced to zero, but still the same phenomenon would occur. This minor energy exchange is even contributing in a negative sense, and does not need to be taken into account to explain the phenomenon.
This is the type of problem we have little reason to consider air resistance. Therefore mentioning one having more area then the other seems inappropriate.
Also I don't think it would make much difference if this was done with sheets of metal. I've never really seen a sheets of metal falling, I wonder what you meant by that?
Check assumptions... "All collisions are perfectly elastic which means NO kinetic energy is lost in the collisions." "Air resistance is negligible."
It sounds really confusing.
please, show, how your solution DOESN'T violate preservation of energy, taking the assumptions given... i can't help noticing that i'm not the only one who thinks that it kind of DOES!... i mean c'mon!!!! if the bloody ball jumped higher than it's initial point, then it must have got the extra energy from somewhere!!! where did it get it from?!! the space? the Holy Spirit? where? coz it can't get any extra energy from the other ball or from the ground (otherwise the "elastic tale" doesn't work)
Log in to reply
Energy from other ball is OK when collision elastic.
Log in to reply
what's the point of just stating that without any proof? would be very nice if you gave any..
"Elastic" simply means that no energy in the system is lost to friction/heat; it doesn't prevent balls within the system from transferring kinetic energy to each other. It would be easier to help if you explained why you think the "elastic" qualifier prevents the little ball from gaining energy from the big ball instead of accusing physics of mysticism.
The little ball got the "extra" energy from the big ball. The big ball will peak before the dropping position, and the amount of potential energy it "loses" compared to its initial peak is equal to the amount of potential energy the little ball "gains" compared to its original peak. In a real-world, only partially elastic environment this wouldn't be quite true because the balls lose some heat energy in the collisions. But with two sufficiently bouncy balls and a hard surface, you can see for yourself that the "help" the little ball gets from the big ball sends it dramatically high.
Log in to reply
you mean this situation must lead to the case when the big ball, having given some extra energy to the small one, will raise up to the altitude lower than the initial one?
This solution doesn't explain anything, you should explain why there's a kinetic energy transfer from the big ball to the small ball at the impact on the ground. Also, as PP wrote, this should be valid also for two metal sheet since there's no air friction and the collision is perfectly elastic. To me the question is not complete, since the final height depends on the rigidity of the balls: with perfectly rigid balls (and why not, we already have perfectly elastic collision and no air resistance) the final height will be 10m.
Log in to reply
I'm probably wrong, but doesn't the perfectly elastic collision kind of imply rigid balls? Or at least imply that it doesn't matter what exactly the material does since the result of the collision is elastic? Small ball doesn't collide with the ground, it collides with Large ball which wants to return to the starting position. Shouldn't this result in decreasing Large ball's maximum height while increasing Small ball's height, regardless of what exactly is happening to the surface of the balls?
Log in to reply
Elastic collision doesn't imply rigid bodies, it only means no energy dissipation. But if you assume perfectly elastic collision and perfectly rigid balls (that's what you usually do in pool-path games), the small ball will hit the big ones when the big ones is inverting the speed because of the ground collision, and for the small ball it's the same to hit the ground since also the big ball is 100% rigid. The two balls will fall with the same speed and since they were touching they remain in contact, the collision happen in the same instant, and for both sphere there won't be deformation, they will only change the sing of their speed. Without friction they will be touching each other and bouncing from ground to 10m forever...
Say balls have radius and mass r , m and R , M , small and big ball correspondingly. Based on energy conservation, both balls will reach the floor falling a total height h = 1 0 − 2 R counting from their center of mass and speed positive downwards
v o = 2 g h
Now the bigger ball will collide first with the ground and since the collision is elastic it will bounce back with reverse speed − v 0 . Immediately afterwards it will collide with the smaller ball , so we take momentum and energy conservation.
m v 0 − M v 0 = m v ′ + M V ′
2 1 m v 0 2 + 2 1 M v 0 2 = 2 1 m v ′ 2 + 2 1 M V ′ 2
Solve the first w.r.t. V ′ , replace in the second and bring the second to standard quadratic form w.r.t. v ′ . Result is
V ′ = M m − M v 0 − M m v ′
v ′ 2 − 2 m + M m − M v 0 v ′ + m + M m − 3 M v 0 2 = 0
Of the two roots only one makes sense since the other one would imply V ′ = − v 0 and v ′ = v 0 so that the balls pass through each other. The solutions are
V ′ = − m + M M − 3 m v 0
v ′ = − m + M 3 M − m v 0
Note that they are both upward and ∣ v ′ ∣ > ∣ V ′ ∣ so it makes physical sense. Now m + M 3 M − m > 1 ∀ M > m so that ∣ v ′ ∣ > ∣ v 0 ∣ . By energy conservation the small ball will rise to a higher height h ′ than h and the large ball will rise to a lower height. Specifically
h ′ = ( m + M 3 M − m ) 2 h
If one wanted to argue without exact calculation one could say that in two-body collisions the lighter object always gains speed and the heavier object always loses speed. Therefore the lighter ball will have greater speed then before the collision and due to energy conservation reach a greater height.
I like this solution a lot: considering the instant after first contact with the ground is important and I like the point where you point out the important factor is greater than 1. You might want to fix a tiny typo: in your simultaneous equations for KE and momentum, in the first equation (for momentum) the second v ′ should be a V ′ .
A much better solution with formula
The trap here is that you would think that the ball cannot bounce higher than the point it starts from because the potential energy has to be equal to the kinetic energy but in this case the mesurement is 10 meters from the ground not the point from which the small ball bounces of from. (the top of the big ball) On top of that, the bigger ball will transfer some of its energy to the smaller one
Oh my goodness... I hope the hamster is OK.
hahaha very nice explanation!
we know that: d i s t a n t + p o w e r > d i s t a n t
If it wasn't for the assumption that the collisions are perfectly elastic, with no conversion from kinetic energy to heat, which a normal ball would leave on the ground after impact, you would not be able to tell exactly without more information. In this case with negligible air resistance, and with all the collisions being perfectly elastic, the small ball in this example, ought to bounce approximately at least as high as it's starting point returning from the first bounce, because only a negligible amount of opposing forces are there to oppose it.
Since The Ball jumps lower, when a double bounce happens, the velocity is distributed to the top, the momentum also distributes to the top, that's why the smaller ball goes higher than before.
The potential energy of the two balls combined must be the same before letting go and when the balls 'float' in the air the second time. Because the small ball is higher than the large one after the first bounce, its potential energy must be higher (it has to compensate for the loss of height of the large ball) and therefore it's higher.
(https://youtu.be/2UHS883_P60)