Even Or Odd?

The product is even if any of the numbers is even. Therefore, if none of them is even, the product would be odd. Let's first figure out the probability of "odd product".

The probability of picking a odd number is 1/2 at the first time. If you picked an odd number, the probability to pick a odd number the second time is 9/19. The probability to pick a odd number the third time is 8/18, or 4/9. Thus, the probability that the product is odd is $\frac{1}{2} \cdot \frac{9}{19} \cdot \frac{4}{9} = \frac{2}{19}.$

That means the probability of "even product" is 1-2/19=17/19.

The product of three integers may only be odd if and only if the chosen integers are all odd.

So the probability of obtaining odd product is 10C3/20C3 =2/19

Then, we subtract it from 1 to get the probability of having an even product. 1-2/19= 17/19

The only way for the product $abc$ to be odd is if all three are odd, so we'll calculate the number of ways to choose three odd numbers from the first 20 positive integers, then take the difference from the total number of combinations.

Formula for choosing three numbers, without replacement, from n options: $\frac{(n)(n-1)(n-2)}{6}$

(n choices, multiplied by n-1 choices, multiplied by n-2 choices. You divide by 6 if you don't care what order the numbers appear in.)

Total number of possible combinations of 3 numbers, without replacement, from 20 options: $\frac{20(19)(18)}{6} = 1140$

Total number of possible combinations of 3 odd numbers, without replacement, from 10 options: $\frac{10(9)(8)}{6} = 120$

Total number of combinations of numbers that meet the requirement of the question: $1140-120 = 1020$ .

Probability of choosing three numbers that give you an even product: $\frac{1020}{1140} = \frac{102}{114} = \frac{17}{19}$ .

From the digits $1-20$ , there are $10$ odd digits and $10$ even digits.

There are four cases.

(even)(even)(even) = even

(even)(even)(odd) = even

(even)(odd)(odd) = even

(odd)(odd)(odd) = odd

Probability that it is odd is, $P=$ $\frac{10C3}{20C3}=$ $\frac{2}{19}$ , therefore, probability that is even is, $P=1-$ $\frac{2}{19}=$ $\frac{17}{19}$

Alternate Solution: consider the three cases with a result of even

$P=$ $\frac{10C3}{20C3}+$ $\frac{(10C2)(10C1)}{20C3}+$ $\frac{(10C1)(10C2)}{20C3}=$ $\frac{17}{19}$

only way of getting an odd number after multiplying 3 times is (ODD X ODD x ODD). Since its without replacement, the probabilities would be 1/2 9/19 8/18 = 2/19. Even would just be 1 - 2/19 = 17/19.

sry didn't noticed the mistake, thanx for hlp.

The probability that the product is even = 1 minus the probability that the product is odd. The product will be odd when all three positive integers are odd. So it boils down to 1 - (10 * 9 * 8) / (20 * 19 * 18) = 17/19.

The only odd product is odd * odd * odd. There are 10 odd numbers between 1 and 20, inclusive.

There are 10-choose-3 = 120 odd sets of three numbers.

There are 20-choose-3 = 1140 totals sets of three numbers.

So the probability of an even number is $\frac{1140-120}{1140}$ = $\frac{1020}{1140}$ = $\frac{17}{19}$ .

since this is the case where we choose the numbers one by one, we can't use again a previously chosen number,

the complementary case is where the three numbers are odd. that is:

$\frac{10}{20} * \frac{9}{19} * \frac{8}{18} = \frac{2}{19}$

so, the probability that we're looking for is : $\boxed{\frac{17}{19}}$

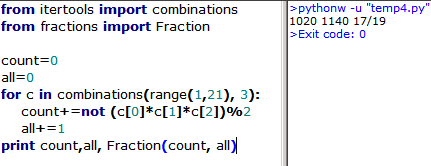
I would suggest that the problem should state that the selections are made without replacement .