Multivalued!

$a^2+b^2+c^2 +2(ab+bc+ca) = (a+b+c)^2$ $ab+bc+ca = - \frac{1}{2} (a^2+b^2+c^2) + \frac{1}{2} (a+b+c)^2$ $ab+bc+ca = - \frac{1}{2} + \frac{1}{2} (a+b+c)^2$

Therefore, to minimize $ab+bc+ca$ , we need to minimize $(a+b+c)^2$ . $(a+b+c)^2 \geq 0$ $\therefore min( (a+b+c)^2 ) = 0$ $\implies a+b+c = 0$

We have the following set of equations now. $a+b+c = 0 \> \implies \> c=-a-b$ $a^2+b^2+c^2 = 1$ $a^2+b^2+(-a-b)^2 = 1$ $b^2 + ab + a^2 - \frac{1}{2} = 0$ $b = \frac{ -a \pm \sqrt{2-3a^2} }{2}$

Also, $c = -a - b$ $c = \frac{ -a \mp \sqrt{2-3a^2} }{2}$

Hence, we get the triple as, $\Bigg( a, \frac{ -a \pm \sqrt{2-3a^2} }{2}, \frac{ -a \mp \sqrt{2-3a^2} }{2} \Bigg)$

As $(a, b, c)$ should be a triple of real numbers, $\sqrt{2-3a^2} \geq 0$ $\implies - \sqrt{\frac{2}{3}} \leq a \leq \sqrt{\frac{2}{3}}$

Notice, we solved for the triple $(a,b,c)$ with respect to $a$ . We could have solved the system with respect to $b$ or $c$ too. Hence, from the symmetry argument: $- \sqrt{\frac{2}{3}} \leq a,b,c \leq \sqrt{\frac{2}{3}}$

Finally, as we can see from the expression of the triple, we can choose any arbitrary $a$ from the range $[ - \sqrt{\frac{2}{3}}, \sqrt{\frac{2}{3}}]$ , and we would get a triple of real numbers which satisfy our conditions. Therefore, we have infinite sets of values.

Starting from the identity ${\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca$ , we get ${\left( {a + b + c} \right)^2} = 1 + 2ab + 2bc + 2ca \Rightarrow ab + bc + ca = \frac{{{{\left( {a + b + c} \right)}^2} - 1}}{2}.$ The expression $\frac{{{{\left( {a + b + c} \right)}^2} - 1}}{2}$ gets minimised when ${\left( {a + b + c} \right)^2}$ does so, that is when $a + b + c = 0$ .
There are infinitely many triples of real numbers to satisfy this.

In fact, due to the restriction given, a solution is any triple that corresponds to the coordinates of a point that belongs to the circle which is the intersection of the plane $z+y+z=0$ ant the sphere $x^2+y^2+z^2=1$ .

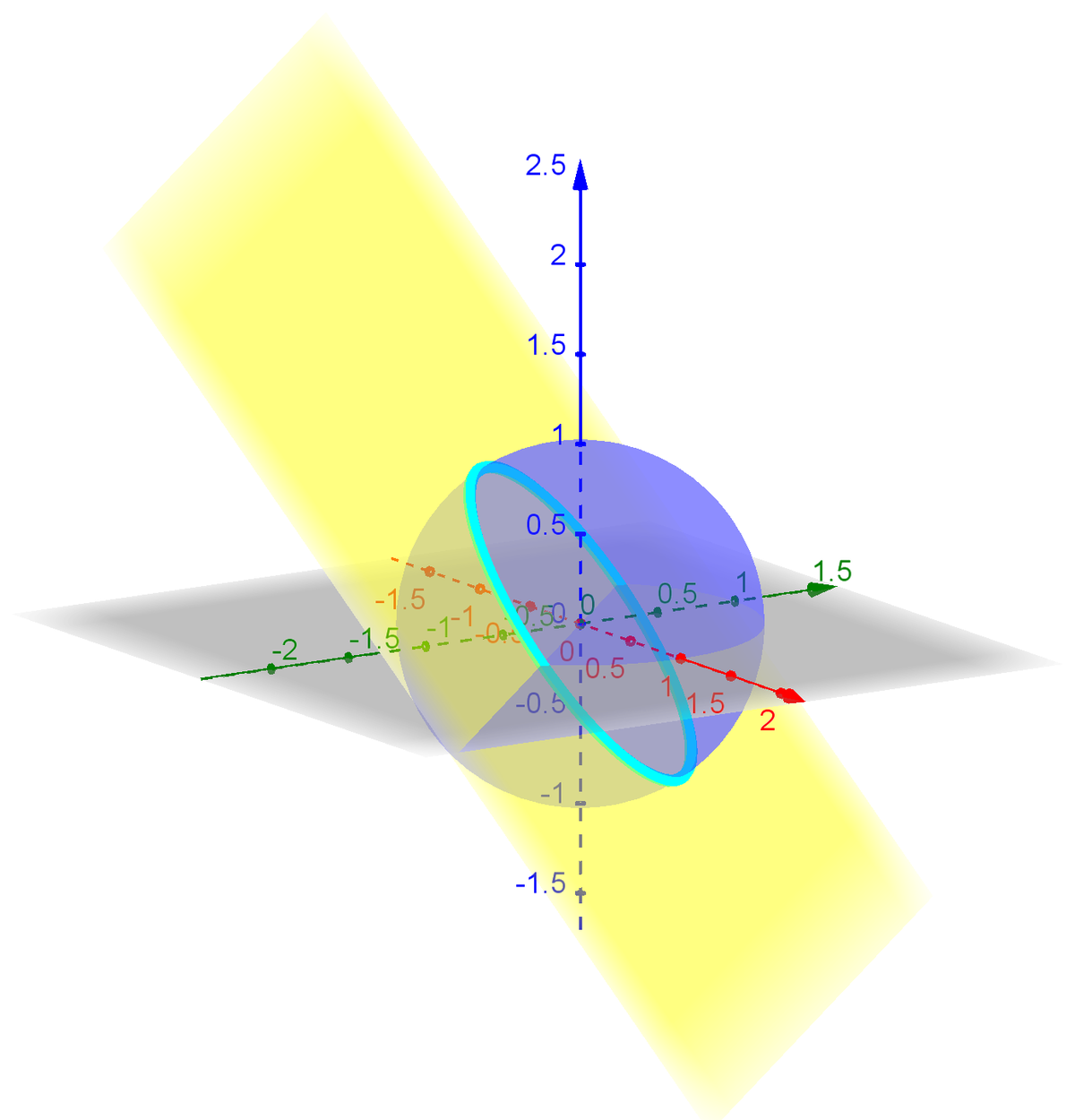
The set of all these triples is $S = \left\{ {\left( { - \frac{1}{{\sqrt 2 }}\cos t + \frac{1}{{\sqrt 6 }}\sin t,\;\frac{1}{{\sqrt 2 }}\cos t + \frac{1}{{\sqrt 6 }}\sin t,\; - \sqrt {\frac{2}{3}} \sin t} \right),\quad t \in \left[ {0,\;2\pi } \right)} \right\}.$

In a different perspective, the solutions may be written as $\left\{ {\left( {k,\;\frac{1}{2}\left( {\sqrt {2 - 3{k^2}} - k} \right),\;\frac{1}{2}\left( { - \sqrt {2 - 3{k^2}} - k} \right)} \right),\quad k \in \left[ { - \sqrt {\frac{2}{3}} ,\;\sqrt {\frac{2}{3}} } \right]} \right\}.$

For some concrete examples, all 6 permutations of $\left( {0,\;\frac{1}{{\sqrt 2 }},\; - \frac{1}{{\sqrt 2 }}} \right)$ are solutions.

Hence, the answer is $\boxed{\text{More than four sets of values of a, b, c}}.$