Pentagon interior point
A regular pentagon has its center at the origin of the Cartesian plane in standard orientation (with one of the vertices lying on the positive y -axis). Its vertices are labelled as shown in the figure below. A point P lies inside it, such that P A = 1 6 , P B = 1 9 , and P C = 1 7 . If ( x , y ) are the coordinates of point P and R is the circumradius of the pentagon, then find ⌊ 1 0 0 0 ( x + y + R ) ⌋ . The figure is drawn to scale.
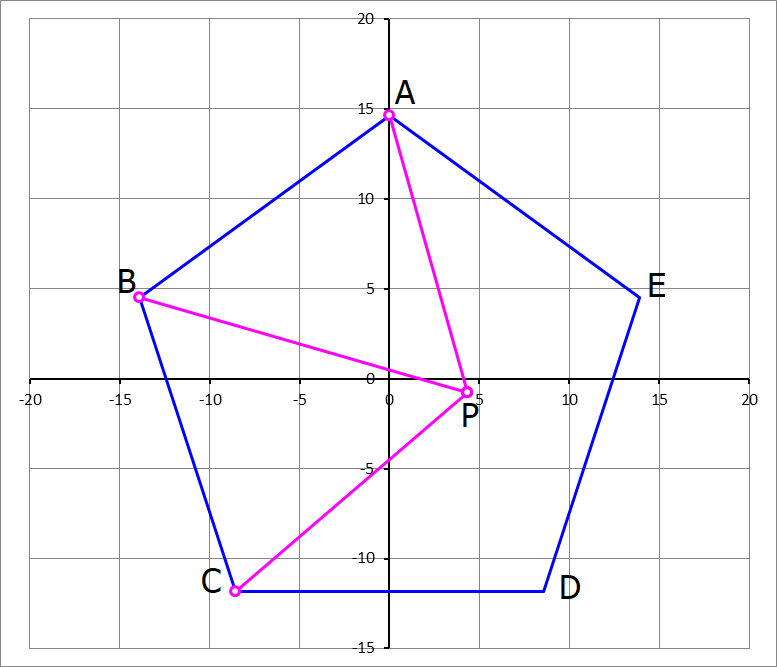
The answer is 18169.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let s be the side of the pentagon. Then by the law of cosines on △ P B A , ∠ P B A = cos − 1 ( 2 ⋅ 1 9 ⋅ 1 6 s 2 + 1 9 2 − 1 6 2 ) , and on △ P B C , ∠ P B C = cos − 1 ( 2 ⋅ 1 9 ⋅ 1 7 s 2 + 1 9 2 − 1 7 2 ) . Since the interior angle of a regular pentagon is 1 0 8 ° , ∠ P B A + ∠ P B C = 1 0 8 ° . These equations solve numerically to s ≈ 5 . 2 0 1 1 5 7 5 6 4 or s ≈ 1 7 . 1 7 0 8 3 8 3 6 . However, if s ≈ 5 . 2 0 1 1 5 7 5 6 4 then point P is outside the pentagon, so s ≈ 1 7 . 1 7 0 8 3 8 3 6 . The circumradius is then R = 2 sin 3 6 ° s ≈ 1 4 . 6 0 6 3 8 7 5 3 .
A 's coordinates are A ( 0 , R ) , and B 's coordinates are B ( R cos 1 6 2 ° , R sin 1 6 2 ° ) . Since P A = 1 6 , x 2 + ( y − R ) 2 = 1 6 2 , and since P B = 1 9 , ( x − R cos 1 6 2 ° ) 2 + ( y − R sin 1 6 2 ° ) 2 = 1 9 2 . When R ≈ 1 4 . 6 0 6 3 8 7 5 3 , these equations solve to x ≈ 4 . 3 5 3 2 7 and y ≈ − 0 . 7 9 0 0 1 , and ⌊ 1 0 0 0 ( x + y + R ) ⌋ = 1 8 1 6 9 .
With R being the circumradius of the pentagon, the 5 vertices (from A to E) are given by,
p k = R u k for k = 1 , . . . , 5 ( 1 )
where u k = ( − sin 5 2 π ( k − 1 ) , cos 5 2 π ( k − 1 ) ) ( 2 )
If we now define p = ( x , y ) to be the coordinate vector of the interior point, then, for i = 1 , 2 , 3 , we have
( p − p i ) T ( p − p i ) = d i 2 ( 3 )
where d 1 = 1 6 , d 2 = 1 9 , d 3 = 1 7 .
Expanding the left hand side of equation (3), gives,
p T p − 2 p T p i + p i T p i = d i 2 ( 4 )
Substituting equation (1) into (4), yields, for i = 1 , 2 , 3 ,
p T p − 2 R p T u i + R 2 = d i 2 ( 5 )
So that,
p T p − 2 R p T u 1 + R 2 = d 1 2 ( 6 )
p T p − 2 R p T u 2 + R 2 = d 2 2 ( 7 )
p T p − 2 R p T u 3 + R 2 = d 3 2 ( 8 )
subtracting (7) from (6), and (8) from (6),
− 2 R p T ( u 1 − u 2 ) = d 1 2 − d 2 2 ( 9 )
− 2 R p T ( u 1 − u 3 ) = d 1 2 − d 3 2 ( 1 0 )
Dividing (9) by (10), eliminates R , and yields, after cross multiplication,
p T w = 0 ( 1 1 )
where,
w = ( d 1 2 − d 3 2 ) ( u 1 − u 2 ) − ( d 1 2 − d 2 2 ) ( u 1 − u 3 ) ( 1 2 )
Since the vector w = ( w x , w y ) is available, equation (11), can be solved directly, to yield,
p = t v ( 1 3 )
where v = ( − w y , w x ) ( 1 4 )
and t is a real scalar parameter to be determined. Substituting equation (13) into (9), yields,
− 2 t R v T ( u 1 − u 2 ) = d 1 2 − d 2 2 ( 1 5 )
from which,
t R = C 0 , where C 0 = ( − 2 v T ( u 1 − u 2 ) ) ( d 1 2 − d 2 2 ) ( 1 6 )
Note that, since R is positive, t has the same sign as C 0 .
Substituting equation (13) into equation (6),
t 2 ( v T v ) − 2 t R v T u 1 + R 2 = d 1 2 ( 1 7 )
using equation (16), this becomes,
t 2 ( v T v ) − 2 C 0 v T u 1 + t 2 C 0 2 = d 1 2 ( 1 8 )
and this can solved for t quite easily (a quadratic equation in t 2 ), so that, from equation (13), this in turn specifies the point p ,
and from equation (16), this also specifies the circumradius R .
The reader may note that, in general, there will be two solutions, but for the distances in this problem, the point p for the other solution lies outside the pentagon, and is therefore considered an extraneous solution.