Mutual Gravity I - Warmup!

Classical Mechanics Level 1

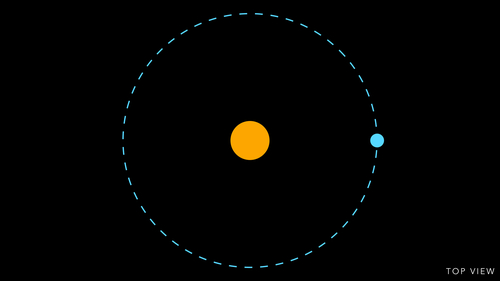Two Spherical Objects of Mass, M attracts themselves for their Mutual Gravitation from a Distance, d

One of them is still ( not moving ) , another is orbiting the first one. Which means first one is at the Focus of the second one's orbit.

So, what's the Orbiting Speed of the second object?

Data:

  1. M = 1 × 1 0 12 k g \text{M}=1\times 10^{12}kg
  2. d = 66.73 m d=66.73m
  3. G = 6.673 × 1 0 − 11 N m 2 k g − 2 \text{G}=6.673\times 10^{-11} \text{N}m^2kg^{-2}


The answer is 1.

Muhammad Arifur Rahman by Muhammad Arifur Rahman , 23, Bangladesh

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The System is alike the Solar System , just the difference is their Mass are equal.

So, You know V 2 = A c c e l e r a t i o n × R a d i u s V^2=Acceleration \times Radius = G M d 2 d =\frac{GM}{d^2}d O r , V = G M d Or, V=\sqrt{\frac{GM}{d}} O r , V = 1 m s − 1 Or, V=1ms^{-1}

Just a typical Problem, in a formal language !

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...