Mutually Common Round Circles
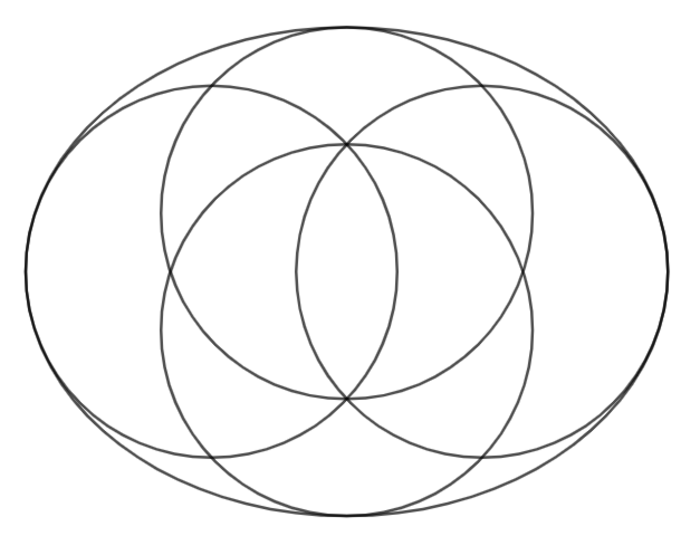
In the ellipse, four identical circles of maximum possible area are positioned, such that two of them whose center lies on the major axis each share one point of tangency with the respective end of the ellipse, and that the other two whose center lies on the minor axis also each share one point of tangency with the respective end of the ellipse. There exists an eccentricity E , such that two intersection points within the minor axis are each formed by three of the four circles.
Input ⌊ 1 0 6 E ⌋ as your answer.
The answer is 649115.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the equation of the ellipse be,
a 2 x 2 + b 2 y 2 = 1 , w h e r e , a > b
Equations of the two circles on whose center lie on the major axis will be,
( x − ( b − r ) ) 2 + y 2 = r 2 a n d ( x − ( − b + r ) ) 2 + y 2 = r 2
The value of r for which the circles are tangent to the ellipse is a b 2 . Hence the two equations become,
( x − a a 2 − b 2 ) 2 + y 2 = a 2 b 4 a n d ( x − a b 2 − a 2 ) 2 + y 2 = a 2 b 4
Solving for the points of intersection, we get,
X = 0 and Y = ± 2 b 2 − a 2
Consider the point ( 0 , − 2 b 2 − a 2 ) , this point must lie on the circle whose center lies on the positive side of the y − a x i s (from intuition). The equation for such a circle is given as,
x 2 + ( y − a a b − b 2 ) 2 = a 2 b 4
Substituting,
( 0 ) 2 + ( − 2 b 2 − a 2 − a a b − b 2 ) 2 = a 2 b 4
Now put b = a 1 − e 2 (where e is the eccentricity of the ellipse) in the above equation.
( − 2 a 2 ( 1 − e 2 ) − a 2 − a 1 − e 2 + a a 2 ( 1 − e 2 ) ) 2 = a 2 a 4 ( 1 − e 2 ) 2
⟹ ( − 2 ( 1 − e 2 ) − 1 − 1 − e 2 + ( 1 − e 2 ) ) 2 − ( 1 − e 2 ) 2 = 0
⟹ ( − 1 − 2 e 2 − 1 − e 2 ) ( − 1 − 2 e 2 − 1 − e 2 + 2 ( 1 − e 2 ) ) = 0
⟹ − 1 − 2 e 2 − 1 − e 2 = 0 or − 1 − 2 e 2 − 1 − e 2 + 2 ( 1 − e 2 ) = 0
Notice that,
− 1 − 2 e 2 − 1 − e 2 = 0 ∀ e ∈ ( 0 , 1 )
Hence, our only option is to find the solutions of,
− 1 − 2 e 2 − 1 − e 2 + 2 ( 1 − e 2 ) = 0
Use MATLAB and ignore the trivial e = 0 solution. We get e = 0 . 6 4 9 1 1 5 5 1 1 2 3 8 8 0 3 . Now ⌊ e × 1 E + 6 ⌋ = 649115 .
1 2 3 4 5 |
|
By Pythagorean theorem on △ O P K ,
O P 2 + O K 2 = P K 2 ⇒ ( 2 R − b ) 2 + ( a − R ) 2 = R 2 ⇔ ( 4 R 2 − 4 b R + b 2 ) + ( a 2 − 2 a R + R 2 ) = R 2 ⇔ 4 R 2 − 4 b R − 2 a R + a 2 + b 2 = 0 ⇔ 4 ( a b 2 ) 2 − 4 b a b 2 − 2 a a b 2 + a 2 + b 2 = 0 ⇔ ÷ a 2 4 ( a b ) 4 − 4 ( a b ) 3 − ( a b ) 2 + 1 = 0 ⇔ ( a b − 1 ) ( 4 ( a b ) 3 − a b + 1 ) = 0 ⇔ a b < 1 a b ≈ 0 . 7 6 0 6 8 9 8 5 3 4 0 2 2 8 3 7 8 4 8 0 2 0 4 0 4 The eccentricity is given by the formula E = 1 − ( a b ) 2 Substituting the value we found for a b , we get E ≈ 0 .6491155112388 .
For the answer, ⌊ 1 0 6 E ⌋ = 6 4 9 1 1 5 .