Mutually tangent line
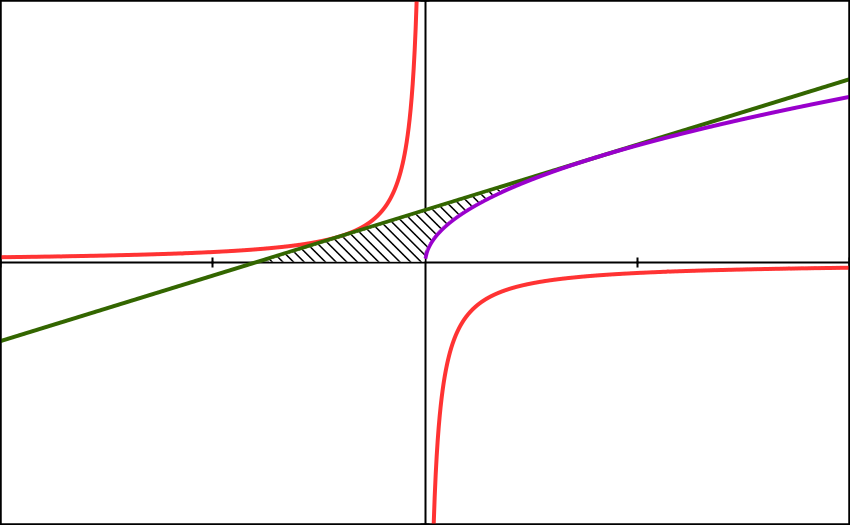
A straight line is drawn in a plane such that it is tangent to both curves and . If the area of the region bound by this line, the -axis and the curve is equal to where and are coprime positive integers, find the value of .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Finding the area by integration is relatively straightforward once the equation of the tangent is known, so I will only explain in detail how I found the equation of the tangent and leave out the details of the integration.
Let the tangent intersect the curve y = − x 1 at the point ( p , − p 1 ) and the curve y = x at the point ( q , q ) .
Since d x d y ( − x 1 ) = x 2 1 , the gradient of the tangent at p is equal to p 2 1 , and the equation of the line in terms of p is given by y = p 2 1 x − p 2 (using y = m ( x − x 0 ) + y 0 ).
Similarly, d x d y ( x ) = 2 x 1 , so the gradient of the tangent at q is equal to 2 q 1 , and the equation of the line is y = 2 q 1 x + 2 q .
Equating coefficients of x and constants we find that
p 2 1 = 2 q 1 and − p 2 = 2 q . Substituting,
p 2 1 = 2 ( − p 4 ) 1
p 2 1 = − 8 p
p 3 = − 8 and hence p = − 2 . Substituting this value into y = p 2 1 x − p 2 we find that y = 4 1 x + 1 .
From here the area is found by evaluating ∫ − 4 0 ( 4 1 x + 1 ) d x + ∫ 0 4 ( 4 1 x + 1 − x ) d x = 3 8 .