My age is everywhere

Calculus Level 5

$\large \displaystyle\int _{ 0 }^{ \infty }{ \dfrac { 1 }{ 1+{ x }^{ 13 } } \, dx } =\dfrac { a }{ b } \pi \csc { \left( \dfrac { \pi }{ c } \right) }$

If the equation above holds true for positive integers $a,b$ and $c$ , with $a,b$ coprime, find $a+b+c$ .

The answer is 27.

2 solutions

Parv Mor
Apr 25, 2016

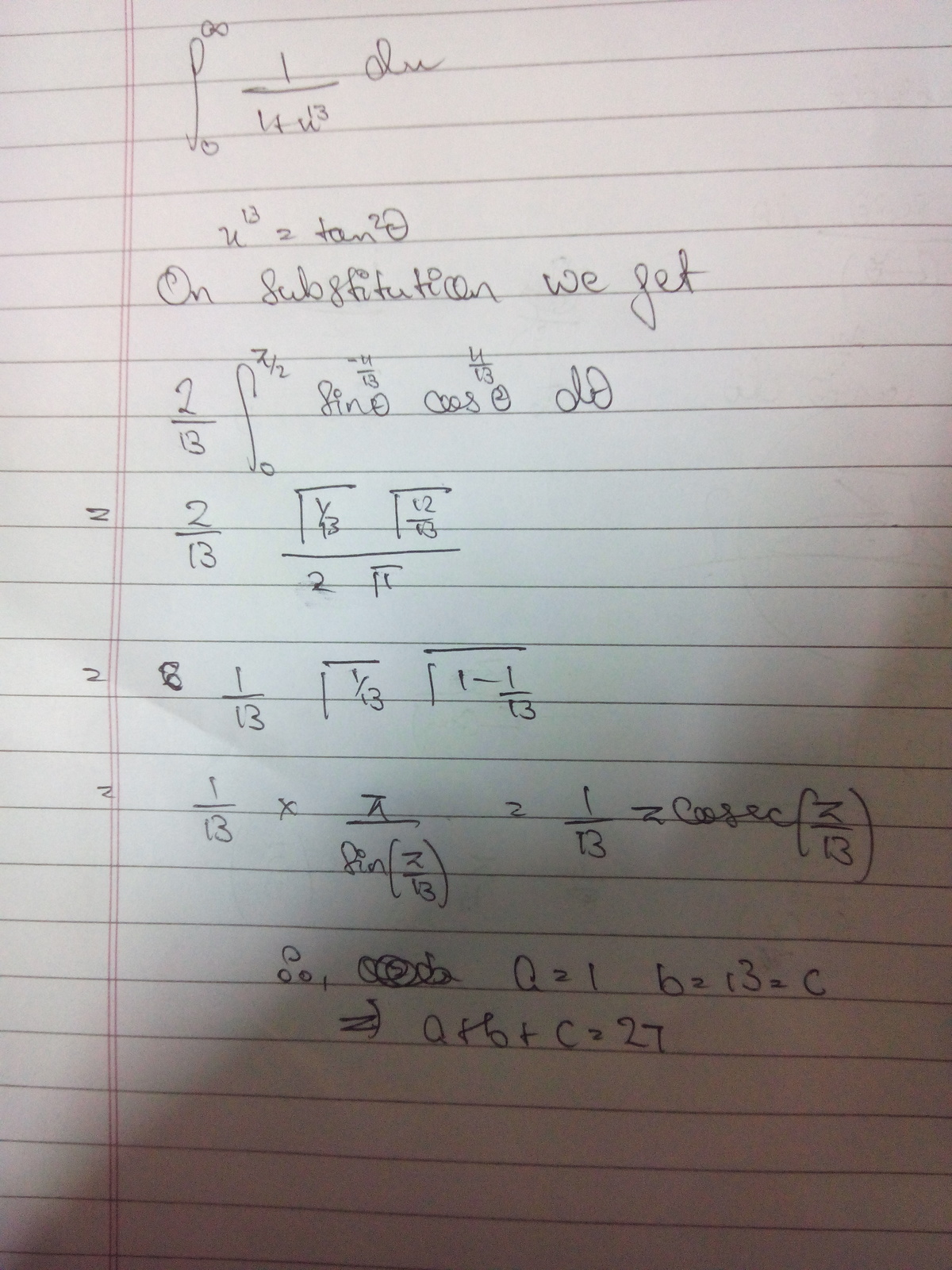
One can use contour Integration to show that $\int x^m/(1+x^n)dx=(π/n)/sin(m+1)π/n.$ with the given set of limits(zero-infinite).For us the integral is simply $π/13csc(π/13)$

Spandan Senapati - 4 years, 1 month ago

First Last
Oct 15, 2016

A beautiful solution I have seen multiple times on Math Stack:

$\displaystyle\int_{0}^{\infty}\frac{1}{x^n+1}dx = \int_{0}^{\infty}\int_{0}^{\infty}e^{-t(1+x^n)}dxdt$

Sub $\displaystyle u = x^nt\quad du = nx^{n-1}t\,dx$

$\displaystyle\frac{1}{n}\int_{0}^{\infty}e^{-t}t^{\frac{-1}{n}}dt\int_{0}^{\infty}u^{\frac{1}{n}-1}e^{-u}du =$

$\displaystyle\frac{\Gamma(1-\frac{1}{n})\Gamma(\frac{1}{n})}{n} = \frac{\pi}{n\sin{\frac{\pi}{n}}}\quad \text{by Euler's Reflection Formula}$

Plug in 13 for $\displaystyle\huge{\color{#D61F06}\frac{\pi}{\color{#3D99F6}13\color{#20A900}\sin{\color{#EC7300}\frac{\pi}{13}}}}$

My age is everywhere

The answer is 27.

2 solutions

0 pending reports