This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
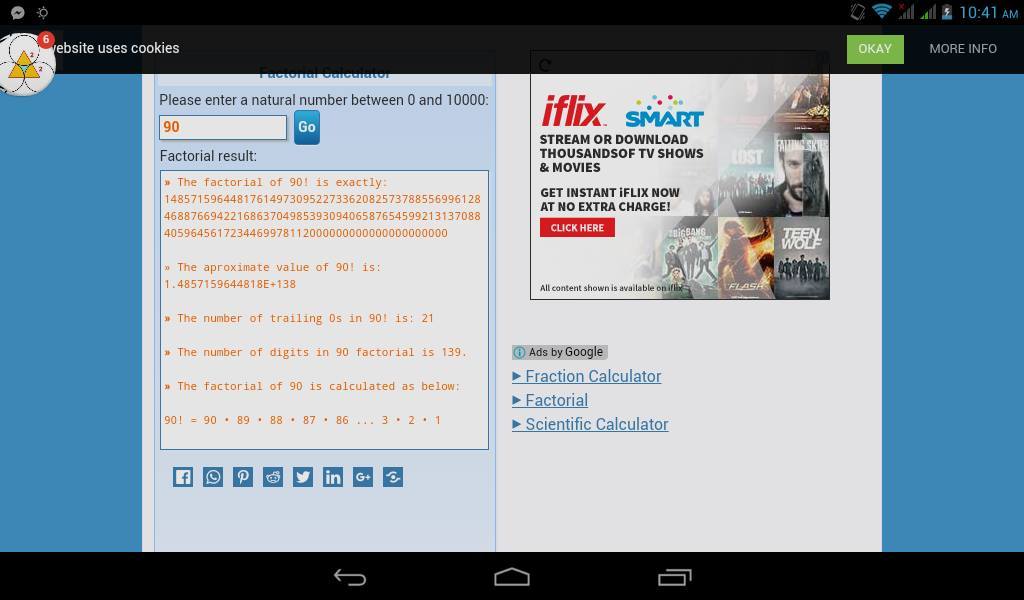
9 0 ! = 1 × 2 × 3 × 4 × 5 × . . . × 8 9 × 9 0
We can rearrange the factors of 90! into:
( 5 × 1 0 × 1 5 × . . . × 8 5 × 9 0 ) × ( 1 × 2 × 3 × 4 ) × ( 6 × 7 × 8 × 9 ) × ( 1 1 × 1 2 × 1 3 × 1 4 ) × ( 1 6 × 1 7 × 1 8 × 1 9 ) × . . . × ( 8 1 × 8 2 × 8 3 × 8 4 ) × ( 8 6 × 8 7 × 8 8 × 8 9 )
Factoring out the 5's,
5 1 8 × 1 8 ! × ( 1 × 2 × 3 × 4 ) × ( 6 × 7 × 8 × 9 ) × ( 1 1 × 1 2 × 1 3 × 1 4 ) × ( 1 6 × 1 7 × 1 8 × 1 9 ) × . . . × ( 8 1 × 8 2 × 8 3 × 8 4 ) × ( 8 6 × 8 7 × 8 8 × 8 9 )
Let us consider (10 a + 1)(10 a + 2)(10 a + 3)(10 a +4) and (10 a + 6)(10 a + 7)(10 a + 8)(10 a + 9)
This expression is a generalized format of the terms (1 \times 2 \times 3 \times 4 ) and (6 \times 7 \times 8 \times 9), respectively.
Simplifying these two expressions, we'll get:
1 0 0 0 0 a 4 + 1 0 0 0 0 a 3 + 3 5 0 0 a 2 + 5 0 0 a + 2 4 and 1 0 0 0 0 a 4 + 3 0 0 0 0 a 3 + 3 3 5 0 0 a 2 + 1 6 5 0 0 a + 3 0 2 4
We can disregard the first four terms because they contain at least 2 trailing zeroes
We can generalize that the last two digits of the terms of the form (10 a + 1)(10 a + 2)(10 a + 3)(10 a +4) and (10 a + 6)(10 a + 7)(10 a + 8)(10 a + 9) is 24 .
Therefore, the last two digits of 90! is equal to the last two digits of 5 1 8 × 1 8 ! × 2 4 1 8 = 5 1 8 × 1 8 ! × 2 1 8 × 2 3 6 × 3 1 8
By observation,
the last digit of ( 2 1 0 ) e v e n is 76
the last digit of ( 2 1 0 ) o d d is 24
the last digit of ( 3 4 ) 1 m o d 5 is 81
the last digit of ( 3 4 ) 2 m o d 5 is 61
the last digit of ( 3 4 ) 3 m o d 5 is 41
the last digit of ( 3 4 ) 4 m o d 5 is 21
the last digit of ( 3 4 ) 5 m o d 5 is 01
Finding the last two digits of 1 8 ! × 2 3 6 × 3 1 8 = > ( 2 1 0 ) 3 × 2 6 × ( 3 4 ) 4 × 3 2 × 1 8 !
= > ( 2 4 ) × 2 6 × ( 2 1 ) × 3 2 × 1 8 ! = > ( 2 4 ) ( 6 4 ) ( 2 1 ) ( 9 ) × 1 8 ! = > 0 4 × 1 8 !
The last two digits of 18! can be solved like how we solved earlier:
( 5 × 1 0 × 1 5 ) × ( 1 × 2 × 3 × 4 ) × ( 6 × 7 × 8 × 9 ) × ( 1 1 × 1 2 × 1 3 × 1 4 ) × ( 1 6 × 1 7 × 1 8 )
= 5 3 × 3 ! × ( 2 4 3 × ( 1 6 × 1 7 × 1 8 ) = > 6 × 5 3 × 2 3 × 1 2 3 × 9 6 = > 6 × 1 2 3 × 9 6
Therefore, the last two digits of 90! is equivalent to the last two digits of 0 4 × 6 × 1 2 3 × 9 6 = 1 2