My first computer programming problem, October 1964 -- taxi distance on a m by n grid.
The problem's question: In particular, on a 10 by 10 grid, how non-backtracking routes between opposite corners?
Assume that you start in the lower left of the grid and are traveling to the upper right of the grid via the streets (lines, edges), how many distinct routes without backtracking (i. e., never traveling to the left or down) are there? The image below illustrates what is meant by a 10x10 (i.e., the streets are what are counted).
At the time I was a first semester first year undergraduate at the University of Iowa, when two Ph. D. students challenged me to solve this problem. I asked for and received permission to use the main university computer to solve the problem, an IBM 7044 with 32768 words of core memory. I was disgusted when I realized just how simple the problem was although it took me 3 weeks to program it in FORTRAN II, see the output, and realize at what I was looking.

The answer is 48620.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
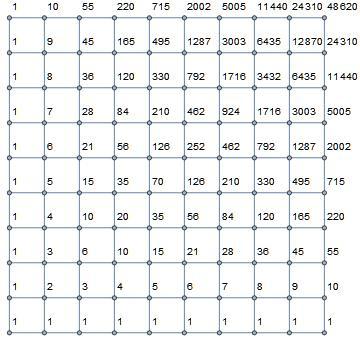
1 8 "moves" are needed to get from the bottom-left to the top-right corner. Of these, 9 must be to the right, and 9 must be up. There are ( 9 1 8 ) = 4 8 6 2 0 distinct ways to do choose these.