My first problem so far, after ten thousand solved
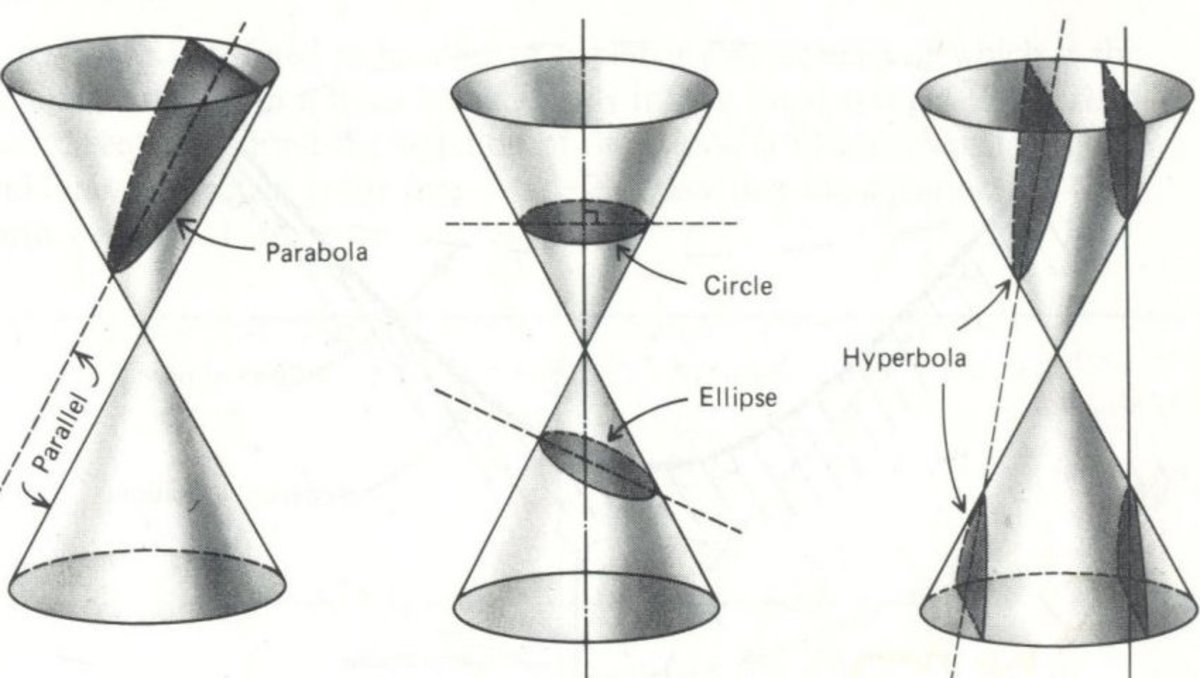Its known that conic section is somehow determined by the different cross section after cutting through a cone with different angle .It's general form could be written as Ax^2+Bxy+Cy^2+Dx+Ey+F=0
If we now randomly picking some value from the field R to determine the value of A,B,C,D,E,F , for which conic section(s) would have theoretically 0 probability to appear?
(1) two distinct real lines (2) parallel lines (3) non-real lines (4) hyperbola (5) rectangular hyperbola (6) parabola (7) circle (8) ellipse
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
When we rewrite the form into ax^2+2hxy+by^2 +2gx +2fy +c =0 , and determine the discernment= abc+2fgh-af^2-bg^2-ch^2 ,(1),(2),(3) scenario will only be produced when discernment equal to 0 ,which is degenerate case suggested by the law of statistic that the probability distribution of exactly equal a value is always 0 .When we look look back into big capital general equation ,if discernment not equal to 0 ,parabola will appear if and only if B^2-4AC=0 ,circle will appear if and only if A=C,B=0 ,rectangular hyperbola will appear if and only if A=-C ,the reason why they are also degenerate is aforementioned.