My, My! What a Pretty Valentine Pool We Have Here!

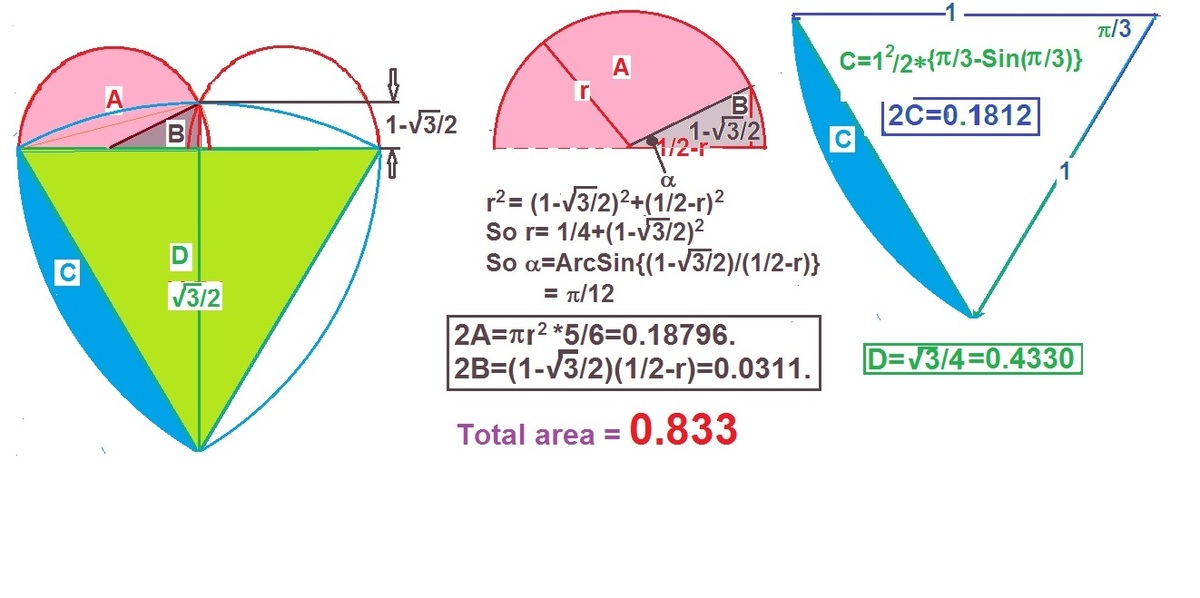
Draw the lines inside $\heartsuit LOVE$ as follow

Circular Sector Area

Angle-chasing, we see that

• Since line $\overline{OE}$ bisects $\angle LEV = 60^{\circ}$ , then $\angle LEO = \angle VEO = 30^{\circ}$ .
• For $|LS| = |SO| = |OR| = |RV|$ , $\overline{HE}$ bisect $\Delta LEO$ and $\overline{TE}$ bisects $\Delta VEO$ . This shows that $\Delta LEO$ and $\Delta VEO$ are both isosceles triangle of base length $1$ .
• Then, $\angle HEO = \angle TEO = 15^{\circ}$ , so $\angle VSE = \angle LSH = \angle LRE = \angle VRT = 75^{\circ}$ . Due to symmetry, $\angle LSO = \angle VRO = 150^{\circ}$

By Law of Cosines , $|LO| = \sqrt{2|LE|^2 - 2|LE|^2\cos\left(30^{\circ}\right)} = \sqrt{2 - \sqrt{3}}$ Therefore, $|LO|^2 = 2|LS|^2 - 2|LS|^2\cos\left(150^{\circ}\right) \quad \Longrightarrow \quad |LS| = \dfrac{\sqrt{2 - \sqrt{3}}}{\sqrt{2 - \sqrt{3}}}$ Thus, since there are two identical angular sector of $150^{\circ}$ with that radius, $A_1 = 2 \cdot \dfrac{5\pi}{12}|LS|^2 = \dfrac{5\pi}{6}|LS|^2 = \dfrac{5\pi}{6} \cdot \dfrac{2 - \sqrt{3}}{2 + \sqrt{3}}$

Triangle Between Sectors

The next step is to determine the area of the triangle, where $|SU| = |RU| = \dfrac{1}{2} - |LS|$ . Since $\Delta LSO = \Delta VRO$ by congruent sides and adjacent angles, $\angle OLV = \angle LVO = 15^{\circ}$ . Because $\Delta LUO$ and $\Delta VUO$ are both right triangles, $|OU| = \dfrac{1}{2}\tan\left(15^{\circ}\right)$ . Therefore, since two triangles $\Delta SUO$ and $RUO$ are both symmetric triangles of congruent areas, $A_2 = |OU| \cdot \left(\dfrac{1}{2} - |LS|\right) = \dfrac{1}{4}\left(7\sqrt{3} - 12\right)$

Sliced Reuleaux Triangle

Before reaching the final step comes the Reuleaux triangle, where the area of minor segment is already "covered" from the previous steps. The area of two minor segments and equilateral triangle of side length $1$ is $\begin{array}{rl} A_3 &= A_{\Delta} + A_{\text{minor}}\\ &= \dfrac{\sqrt{3}}{4} + 2\left(\dfrac{\pi}{6} - \dfrac{\sqrt{3}}{4}\right) \end{array}$

Final Answer

Combining $A_1$ , $A_2$ and $A_3$ gives $\dfrac{1}{6}\left(\sqrt{3} - 2\right)\left(9 + \left(3\sqrt{3} - 14\right)\pi \right)$ , which is about $\boxed{0.833}$ .

Choose a coordinate system with the origin in the midpoint of $LV$ , the $x$ -axis along $LV$ and the $y$ -axis along $EO$ . Then we have the coordinates $L(-\tfrac12,0);\ V(\tfrac12,0);\ E(0,-\tfrac12\sqrt 3),$ and the unit circles obey the equations $(x\pm\tfrac12)^2 + y^2 = 1;\ x^2 + (y+\tfrac12\sqrt 3)^2 = 1.$ Substitute $x = 0$ in the last equation immediately gives the coordinates $O(0,1-\tfrac12\sqrt 3).$ The small circles have centers $(\mp a,0)$ and radius $r$ ; points on these circles obey $(x\pm a)^2 + y^2 = r^2,$ and substituting points $L$ and $V$ immediately gives $a = \tfrac12-r$ ; substituting point $O$ shows that $r = 2-\sqrt 3;\ a = \sqrt 3 - 1\tfrac12.$

To find the area, I intergrated numerically by considering horizontal strips:

• Bottom of heart ( $y < 0$ ): edges of strip are $x = \pm\sqrt{1-y^2}\mp\tfrac12$ .

• Top of heart: edges of strip are $x = \pm a \pm \sqrt{r^2 - y^2}$ . For the "V" in the top of the heart, subtract the part between $x = \pm a \mp \sqrt{r^2-y^2}$ , if positive.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

double r = 2 - sqrt(3);
double a = 0.5 - r;

double dy = 0.0001;
double area = 0;

for (double y = -1; y < r; y += dy) {        

    if (y < 0) {    // bottom of heart
        double xL = sqrt(1 - y*y) - 0.5;
        if (xL > 0) area += 2*dy*xL;
    } else {        // top of heart
        double xS1 = a - sqrt(r*r - y*y);
        double xS2 = a + sqrt(r*r - y*y);
        area += 2*dy*xS2;
        if (xS1 > 0) area -= 2*dy*xS1;
    }
}

out.println(area);

The result: $\boxed{0.833}237$ is precise enough for the three-decimal requirement.