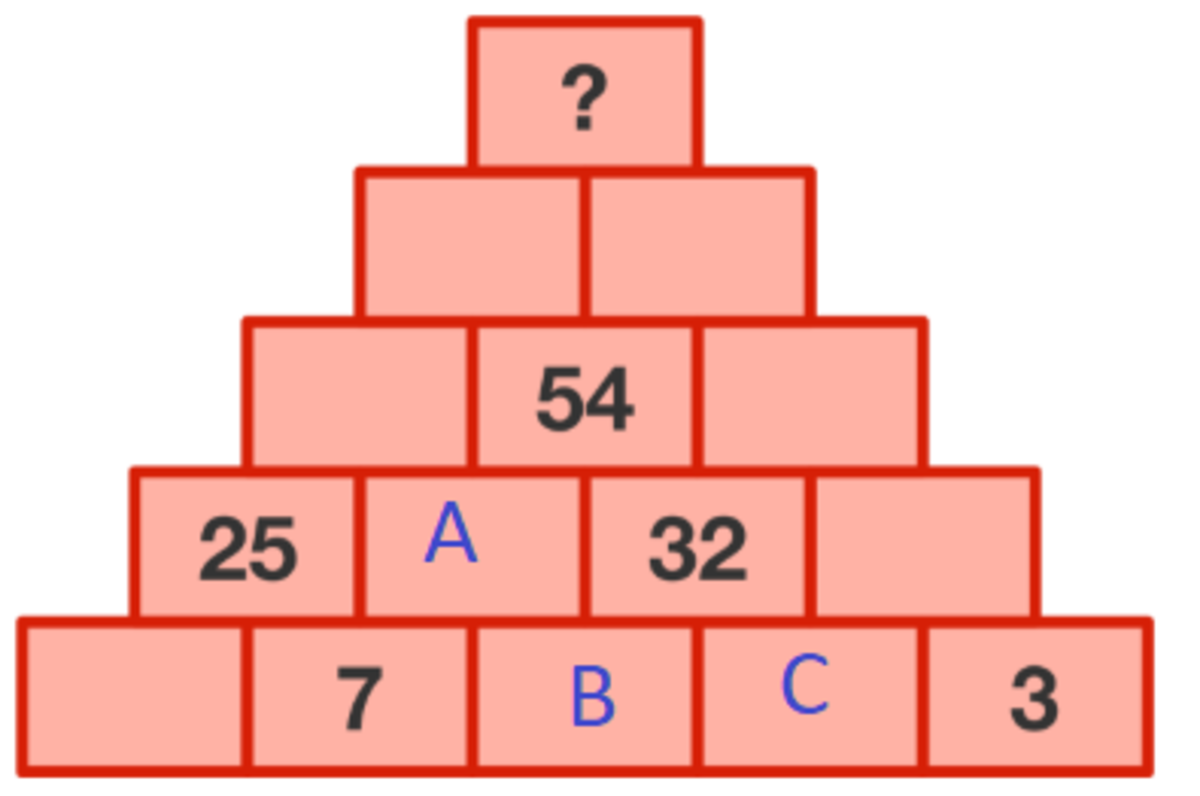
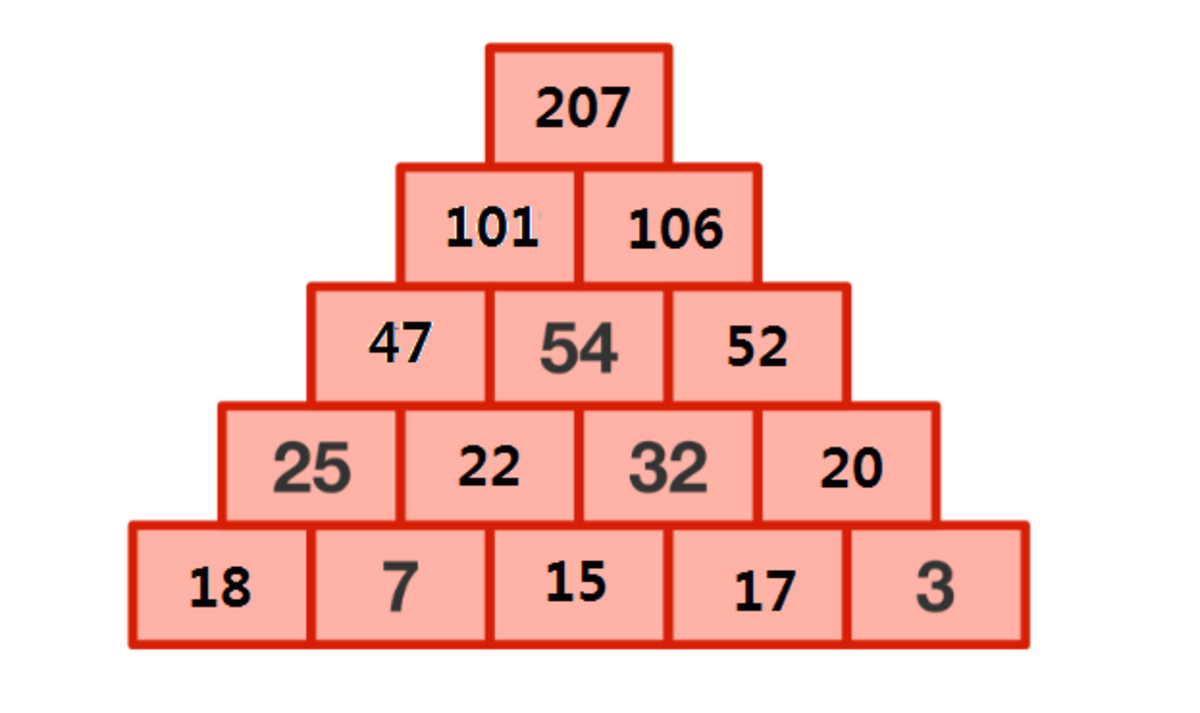
Brick puzzle
In this brick puzzle, the value of a brick must be the sum of the two bricks below it:
What is the value of the top brick?
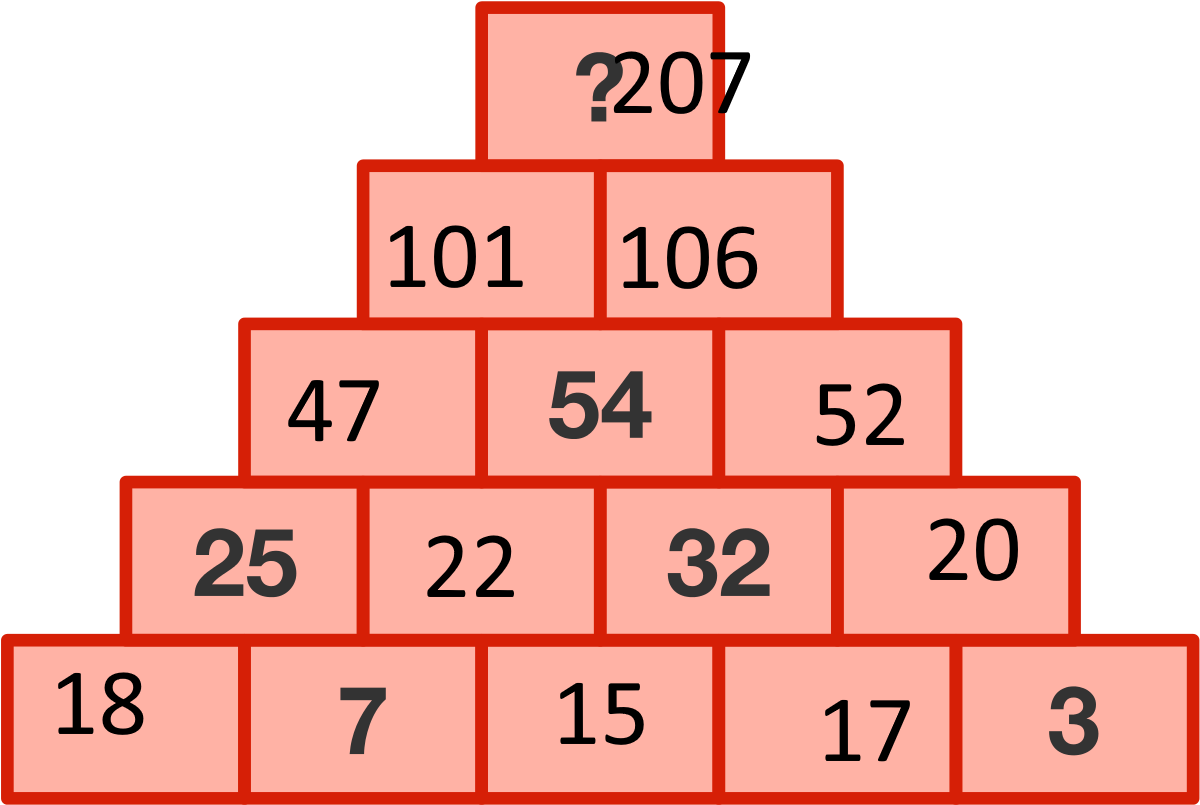
The answer is 207.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
I agree with you.I do that way either
Damn! On (8) I added it up wrong! If it wasn’t for that I would have got it. Oh well :/ Thanks this was very helpful ^u^
Ask me about spelling, grammar, simple fractions. I never took anything but basic math & accounting.
I added 3 and 17 three times and got 30! Silly me
Put a through e in the bottom blocks and solve the system of equations, brute force method. B=7, E=3, A+B=25, C+D=32, B+2C+D=54.
Note the top block is A+4B+6C+4D+E, following pascals triangle.
rref( [0,1,0,0,0,0,7], [0,0,0,0,1,0,3], [1,1,0,0,0,0,25], [0,0,1,1,0,0,32], [0,1,2,1,0,0,54], [1,4,6,4,1,-1,0])
This is what I did to double check my arithmetic. The bottom row is 18, 7, 15, 17, 3 and 18 1+7 4+15 6+17 4+3*1=207
Can you show me how does this link with the Pascal triangle using definitions and formulas?
I'm aware that the coefficients of this is the same as the ones in the triangle and the use of those coefficients to calculate the result is without any flaws. But i wonder is how this could happen and is there a solid mathematical proof to it ? Thanks a lot.
That's correct
The two boxes below the 32 add up to 32. This means the boxes either side of the 32 add up to 7 + 3 2 + 3 = 4 2 . From this, the boxes either side of the 54 add up to 2 5 + 3 2 + 4 2 = 9 9 . And so the two boxes above must add up to 9 9 + 5 4 + 5 4 = 2 0 7 .
 If you find A, B, and C, you're almost done. So A=53-32=22, B=22-7=15, and C=32-15=17. Then just sum up to the top to get 207.
If you find A, B, and C, you're almost done. So A=53-32=22, B=22-7=15, and C=32-15=17. Then just sum up to the top to get 207.
I tried solving this by programming, took me a couple of hours to come up with this JavaScript program that solves this:
var bricks = [[],[],[undefined,54],[25,undefined,32],[undefined,7,undefined,undefined,3]]; var brick = (x,y,track) => { if(x<0||y<0||y>x||x>4)return; if(bricks[x][y])return bricks[x][y]; if(!track)track = []; if(track.some(([ex,ey])=>ex===x&&ey===y))return; var getBrick = (X,Y) => brick(X,Y, track.concat([[x,y]])); var solutions = [getBrick(x-1,y)-getBrick(x,y+1),getBrick(x-1,y-1)-getBrick(x,y-1),getBrick(x+1,y)+getBrick(x+1,y+1)]; return solutions.find(sol=>!isNaN(sol)); }; brick(0,0);
Let's start with the bottom row. 25-7=18, so the bottom left must be 18 but that's not important.
Name the number to the right of 7 'a' and the number to the left of 3 'b'.
Next up, the first blank is 7+a. 32 is a+b (this will be important later), and the last blank is 3+b.
Next, the first blank is 25+7+a=32+a. The last blank is 32+3+b=35+b.
Next, the left is 54+32+a=86+a. The right is 54+35+b=89+b.
The top is now 86+89+a+b, we know from before that a+b is 32 so the final result is 86+89+32=207.
Nice done!
Here is a solution that only solves the top value and makes no attempt to solve any of the other 9 unknowns.
2 0 7 = 2 5 + 7 + 2 ( 3 2 ) + 2 ( 5 4 )
The intuition is that the solution must be less than or equal to twice the sum of the values.
? < = 2 ( 5 4 + 3 2 + 2 5 + 7 + 3 )
This can be seen by looking at the middle row, which provides this as the solution:
? = L + 2 ( 5 4 ) + R
So the question is what is L (Left) and what is R (Right).
The Left value is:
L = 2 5 + 7 + ( 3 2 − x )
The Right value is:
R = 3 2 + 3 + ( 3 2 − ( 3 2 − x ) )
Of course we would swap which side has 3 2 − ( 3 2 − x ) and which side has 3 2 − x . However it makes no difference for this purpose. The main point is that each side has some unknown part of 32.
Thus we have:
? = 2 5 + 7 + ( 3 2 − x ) + 2 ( 5 4 ) + 3 2 + ( 3 2 − ( 3 2 − x ) )
Which is simplified:
? = 2 5 + 7 + ( 3 2 − x ) + 2 ( 5 4 ) + 3 2 + ( 3 2 − ( 3 2 − x ) )
? = 2 5 + 7 + 3 2 − x + 2 ( 5 4 ) + 3 2 + 3 2 − ( 3 2 − x )
? = 2 5 + 7 + 3 2 − x + 2 ( 5 4 ) + 3 2 + 3 2 − 3 2 + x
? = 2 5 + 7 + 3 2 + 2 ( 5 4 ) + 3 2 + 3 2 − 3 2
? = 2 5 + 7 + 3 2 + 2 ( 5 4 ) + 3 2
? = 2 5 + 7 + 2 ( 3 2 ) + 2 ( 5 4 )
? = 2 0 7
Here's my solution, with the grid all filled in with the corresponding numbers:
-
I solved it just by finding third number in triangles (adding or subtracting).
Somebody mentioned a program to solve it. I wrote a simple program
in Just Basic which uses the same method:
'pyramid p(rw,ps)
' moving a triangle ABC from the bottom up and left to right
'C
'A B
' and solving it: C=A+B or A=C-B or B=C-A
'prep
dim p(5,5)
'populate given numbers
p(3,2)=54
p(4,1)=25:p(4,3)=32
p(5,2)=7 :p(5,5)=3
print" Initial State ":gosub [print]
'Main program
for pass=1 to 4
print " Pass # ";pass
gosub [MoveABC]
gosub [print]
next pass
END ' of main program
[MoveABC]
for row=5 to 2 step-1
for pos=4 to 1 step-1
'populate triangle ABC
A=p(row,pos):B=p(row,pos+1):C=p(row-1,pos)
'solve it
gosub [SolveABC]
next pos
next row
return
[SolveABC]
if A<>0 and B<>0 and C=0 then C=A+B:p(row-1,pos)=C:goto [rtn]
if A<>0 and B=0 and C<>0 then B=C-A:p(row,pos+1)=B:goto [rtn]
if A=0 and B<>0 and C<>0 then A=C-B:p(row,pos)=A:goto [rtn]
[rtn] return
[print]
for v=1 to 5
for h=1 to 5
print tab(5*h+3);p(v,h);
next h
print
next v
print"-----------------------------------"
return
For those that got it wrong, the order of doing it is irrelevant, all that matters is that you follow the rules and establish the known's (you must know 2 of any 3 part triangle, either the answer and one of the calculations (ie answer 25, calculation 7 + ?) or the 2 calculations (ie 25+22=?), the only 2 you can solve from the start are 18 and 22, these then allow for you to solve 47 and 15, the next are 101 and 17, from here you can only solve 1 box at a time needing that answer to then proceed, 20, 52, 106 and finally 207, see pics already created for graphical reference
See my answer for another method of solving it. You can solve algebraically for just top value.
I treated it like a Sudoku of sorts, start with what you know then fill in the gaps. 32 and ? = 54, then fill in the rest from there!
From a triangle make as 2 numbers and 1 blank, we can solve blank. And when we fill all blank, we get answer. That's my answer:

Anyone have a general solution?
Specifically, can anyone show that, while the question poses no limitations on the types of numbers available (i.e. integers), the solution is unique even for addition over more inclusive sets (e.g. Reals)?
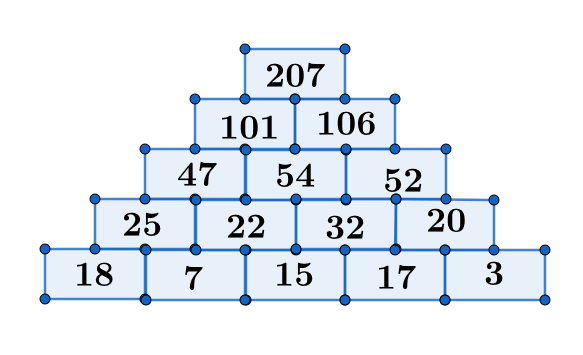

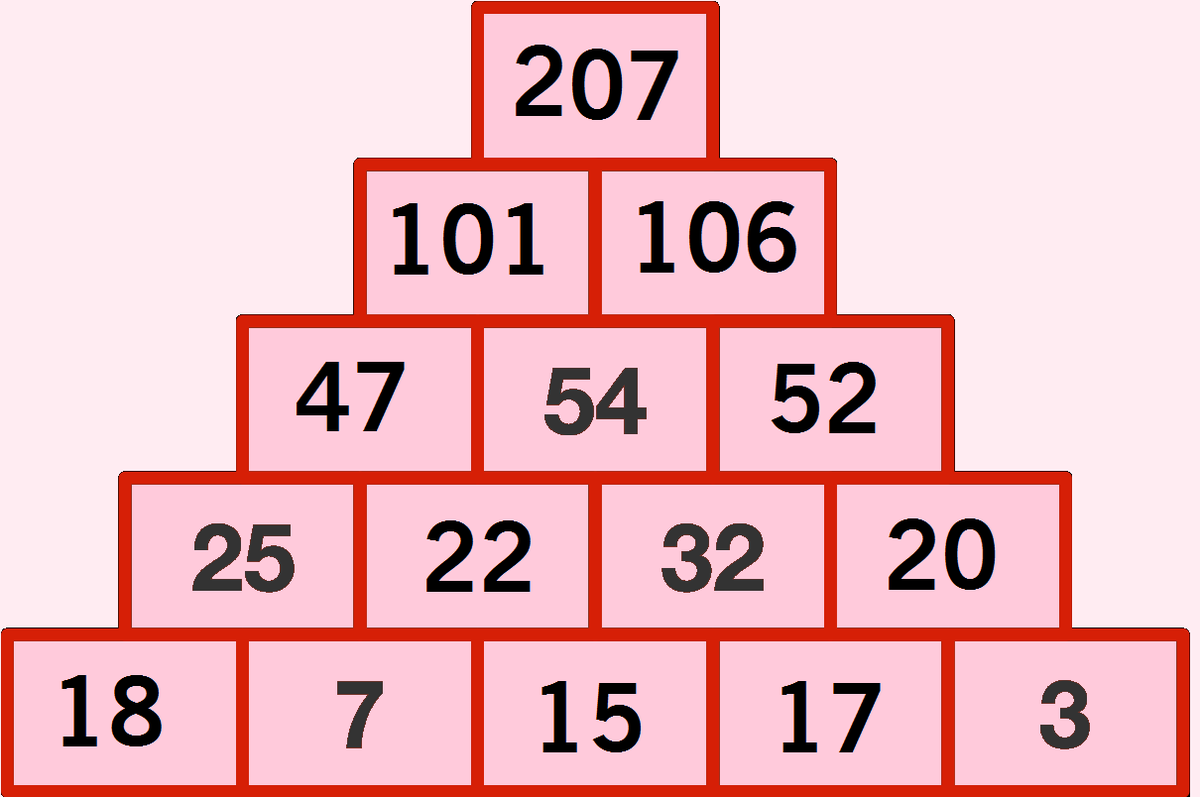
The following diagram shows the final solution, with the number in brackets indicating the order in which they were placed. Note that there are a few slightly different orders to place the digits in, and the 18 in the bottom left needn't be placed at all!