My Science Problems (Part-1)
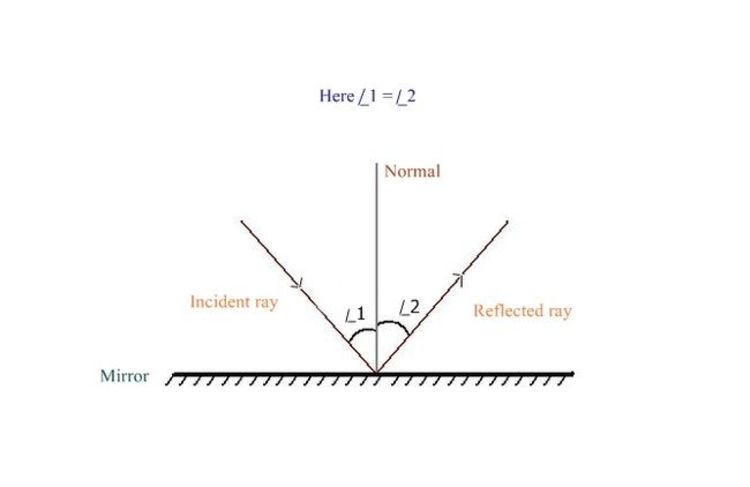We are all familiar with laws of reflection of light.
Now here is the problem,
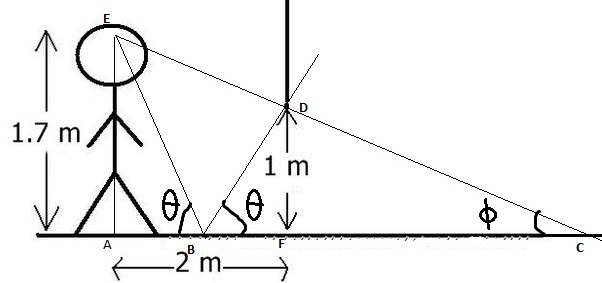
A boy standing on floor made of mirror has a wall infront of him which is hollow from bottom.(as shown in the figure)
Find the maximum length (in metres) of mirror that this boy can utilise to see anything on the other side of wall.
Details and Assumptions:
Consider the eye distance from ground to be equal to height of boy.
The answer is 3.59.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
t
a
n
θ
=
A
B
A
E
=
B
F
D
F
=
A
B
+
B
F
A
E
+
D
F
=
2
1
.
7
+
1
⇒
θ
=
5
3
.
4
7
o
&
tan
ϕ
=
A
C
A
E
=
F
C
D
F
=
A
C
−
F
C
A
E
−
D
F
=
2
1
.
7
−
1
⇒
ϕ
=
1
9
.
2
9
o
A
n
s
=
B
C
=
A
C
−
A
B
=
tan
ϕ
1
.
7
−
tan
θ
1
.
7
=
3
.
5
9
Two things are to be concerned. First one is maximum limit on the mirror from where light can reach eyes. It can be equated by constructing a triangle joining the bottom pt of middle wall and the eye. This distance ( calculated from similarity) comes to be60/7 m. Now the second part. Upto certain distance nothing from other side reaches our eyes through the mirror. It can be calculated again forming two similar triangles by joining the bottom pt of wall to the desired pt and eyes to the desired pt of the mirror. It comes out to be=[2-(1.35)^(-1)]m. Hence the required distance comes out as=3.598 m.