Awesome geometry -5
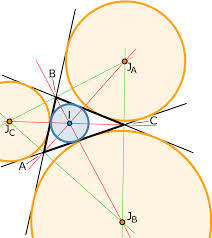 In
△
A
B
C
,
A
C
=
1
3
,
B
C
=
1
4
,
A
B
=
1
5
.
In
△
A
B
C
,
A
C
=
1
3
,
B
C
=
1
4
,
A
B
=
1
5
.
If points J A , J B , J C , are the ex-centers and point I is the in-center of △ A B C . Then find area of △ J A J B J C
Details and Assumptions :-
∙ The asked area is of triangle having vertices J A , J B , J C .
The answer is 341.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Exactly the same!
L
e
t
M
b
e
t
h
e
m
i
d
−
p
o
i
n
t
o
f
B
C
.
T
r
i
a
n
g
l
e
A
B
C
i
s
m
a
d
e
u
p
o
f
t
w
o
t
r
i
a
n
g
l
e
s
C
A
M
=
1
3
.
1
2
.
5
a
n
d
B
A
M
=
1
5
.
1
2
.
9
.
∴
a
r
e
a
A
B
C
,
Δ
=
1
/
2
∗
1
4
∗
1
2
=
8
4
.
2
s
=
a
+
b
+
c
=
4
2
.
A
r
e
a
t
r
i
a
n
g
l
e
J
A
J
B
J
C
,
Δ
J
=
2
∗
r
2
∗
s
a
b
c
∗
Δ
=
(
2
∗
r
)
∗
(
r
∗
s
)
a
b
c
∗
Δ
=
2
∗
r
a
b
c
=
2
∗
2
∗
2
∗
s
Δ
a
b
c
=
4
∗
8
4
1
4
∗
1
3
∗
1
5
∗
4
2
=
3
4
1
.
2
5
.
Sorry I missed the link where I got the formula. I will post it as soon as I find it.
If S is the area of △ABC and S(J) is the area of △J(A)J(B)J(C), the nice equality holds: r·S(J) =2R·S . Here r,R represent the radius of the in-circle and the circumcircle of △ABC respectively. And then we can write S(J) as an algebraic expression of a,b,c (which are the sides of △ABC) easily.
In the given image I have plotted the triangle on the Cartesian plane and found out the coordinates of the ex-centers.
Here the formula for ex-centers in a △ A B C with A ( x 1 , y 1 ) , B ( x 2 , y 2 ) and C ( x 3 , y 3 ) & a = B C , b = C A and c = A B ,
J A = ( − a + b + c − a x 1 + b x 2 + c x 3 , − a + b + c − a y 1 + b y 2 + c y 3 )
Now we could have figured out the are by Area formula.