My Problem Number 6

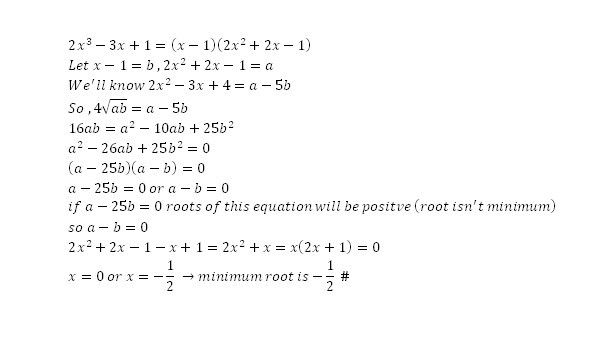
I know this way is a bit too tedious, but I'm posting this anyway.

For all $x \ne \pm 1$ , multiplying both sides by $2(x^2-1)$ we get:

$3(x-2)+4 \sqrt {2x^3-3x+1} = 2(x^2-1)$

$\Leftrightarrow 4 \sqrt {2x^3-3x+1} = 2x^2-3x+4$

As $2x^2-3x+4 > 0$ for all real $x$ , we can square both sides:

$16(2x^3-3x+1)=(2x^2-3x+4)^2$

$\Leftrightarrow 16(2x^3-3x+1)=4x^4-12x^3+25x^2-24x+16$

$\Leftrightarrow 4x^4-44x^3+25x^2+24x=0$

$\Leftrightarrow x(2x+1)(2x^2-23x+24)=0$

Two roots of $2x^2-23x+24$ are both positive because their sum is $\frac {23} {2} > 0$ and their product is $12 > 0$ Hence the minimum root is $x=\boxed {-\frac {1} {2}}$