My Science Problems (Part 4)
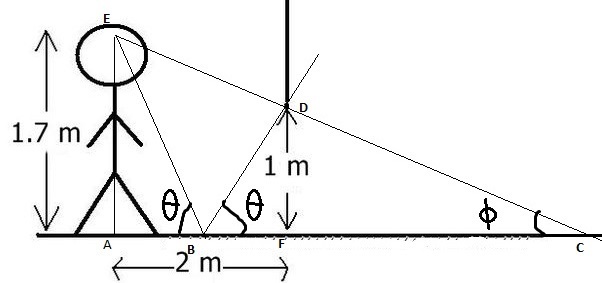
A boy standing on floor made of mirror has a wall in front of him which is hollow from bottom (as shown in the figure).
Let the maximum mirror that this boy can utilize to see anything on the other side of wall has endpoints P and Q .
Find sum of angle of incidences (in degrees) made by two (separate) light rays falling on P and Q .
Give your answer up to 2 decimal places.
Details and Assumptions
Consider the eye distance from ground to be equal to height of boy.
The answer is 107.24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
t
a
n
θ
=
A
B
A
E
=
B
F
D
F
=
A
B
+
B
F
A
E
+
D
F
=
2
1
.
7
+
1
⇒
θ
=
5
3
.
4
7
o
,
tan
ϕ
=
A
C
A
E
=
F
C
D
F
=
A
C
−
F
C
A
E
−
D
F
=
2
1
.
7
−
1
⇒
ϕ
=
1
9
.
2
9
o
I
n
c
i
d
e
n
t
a
n
g
l
e
s
a
r
e
9
0
o
−
θ
&
9
0
o
−
ϕ
s
o
t
h
e
i
r
s
u
m
,
A
n
s
=
1
8
0
o
−
θ
−
ϕ
=
1
0
7
.
2
4
o