Keep Your Alphabet Straight Here
Let a , b , c , and d be real numbers such that a 2 + b 2 = 1 , c 2 + d 2 = 1 , and a c + b d = 0 . Determine a b + c d .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
nice solution!!!
I just plugged in values a= 0, b =1, d = 0, and c = 1 since those are the only numbers that can work.
NO! It's wrong! (bc + ad)x0=0 It's not mean bc + ad = 0. Moreover, the question is ab + cd. The answer can not have only one answer.
Log in to reply
But the algebraic steps have shown that a b + c d = ( b c + a d ) × 0 = 0 , which is true no matter what b c + a d happens to be. I haven't made any assumptions or conclusions as to what b c + a d might be, nor does it matter.
I considered (a,b) and (c,d) as points on a unit circle. I realized that ac + bd = 0 implies that the vectors (a,b) and (c,d) were perpendicular. This means that (c,d) = (-b,a) [ or (-a,b) ] and when you substitute into the desired expression, you get zero.
Cj Esag, you and I think alike!
Note that the third equation implies a 2 c 2 = b 2 d 2 .
Multiply the first equation by d 2 to get: a 2 d 2 + b 2 d 2 = d 2 a 2 d 2 + a 2 c 2 = d 2 By the second equation, this simplifies to a 2 = d 2 .
By the first equation, a and b cannot both be zero. Suppose without loss of generality that a = 0 . Then by the third equation we have c = a − b d
a b + c d = a b + d ( a − b d ) = a b ( a 2 − d 2 ) = 0
a = -1 or 1 and b = 0, or
a = 0 and b = -1 or 1, and
c = -1 or 1 and d = 0, or
c = 0 and d = -1 or 1, therefore
ab = 0 and cd = 0
ab + cd = 0
We aren't given that ( a + b ) 2 = 1 , only that a 2 + b 2 = 1 , so it is not necessarily the case that a 2 + 2 a b + b 2 = 1 . Similarly for ( c + d ) 2 .
Without fancy solutions, note that a and b behave symmetrically. Imagine you have boxes for each variable. If you switch the order of the boxes in the equations with the squares and keep that switch in mind for the multiplication equation, the answer is just a rearrangement of the boxes.
Or you could also set a range for each variable and do 500^4 with a random distribution over the ranges. Then calculate the probability of the equation being false after 500^4 positive tests and use that to sleep at night.
Wow! Wait, what???
My method is more long-winded than the others, but this was the way I thought of:
a^2 + b^2 = 1 (I)
c^2 + d^2 = 1 (II)
ac + bd = 0 (III)
ab + cd = x (IV)
Find x.
Try introducing new variables. WLOG:
let a = cosT, b = sinT, (from (I))
c = cosS, d = sinS. (from (II))
(III):
0 = cosTcosS + sinTsinS
= cos(T - S).
T - S = (2n+1)pi/2 with n being an integer.
Dealing with cos and sin so only need to consider T - S = +- pi/2.
S = T +- pi/2.
(IV):
x = cosTsinT + cosSsinS
= (1/2)[sin2T + sin2S]
= (1/2)[sin2T + sin2(T+-pi/2)]
= (1/2)[sin2T + sin(2T+pi)] or (1/2)[sin2T + sin(2T-pi)]
= 0 or 0
= 0.
You may use trigonometric relations. Clearly, if a=cos x, then b=sin x. Also, if c=cos y, then d=sin y.
Notice, however, that ac+bd=cos x cos y + sin x sin y=cos (x-y). Now it follows that x=y+n pi/2. We'd like to compute
ab+cd=cos x sin x + sin y cos y
Nice way! But can you make a full solution?
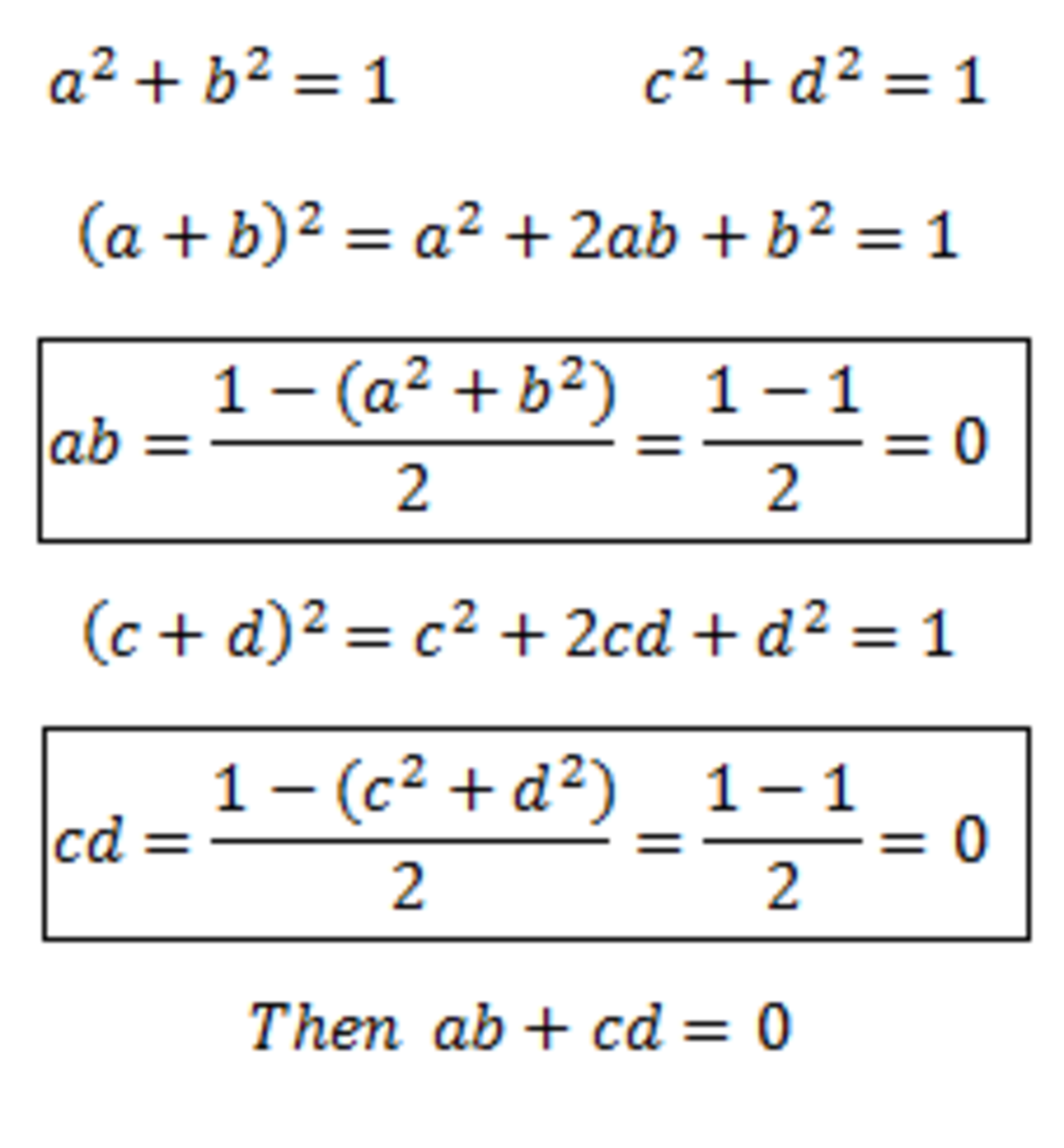
Since a 2 + b 2 = c 2 + d 2 = 1 and a c + b d = 0 we have that
a b + c d = a b ( c 2 + d 2 ) + c d ( a 2 + b 2 ) = a b c 2 + a b d 2 + c d a 2 + c d b 2 =
b c ( a c + b d ) + a d ( b d + a c ) = ( b c + a d ) ( a c + b d ) = ( b c + a d ) × 0 = 0 .