My ultimate Sangaku part 2
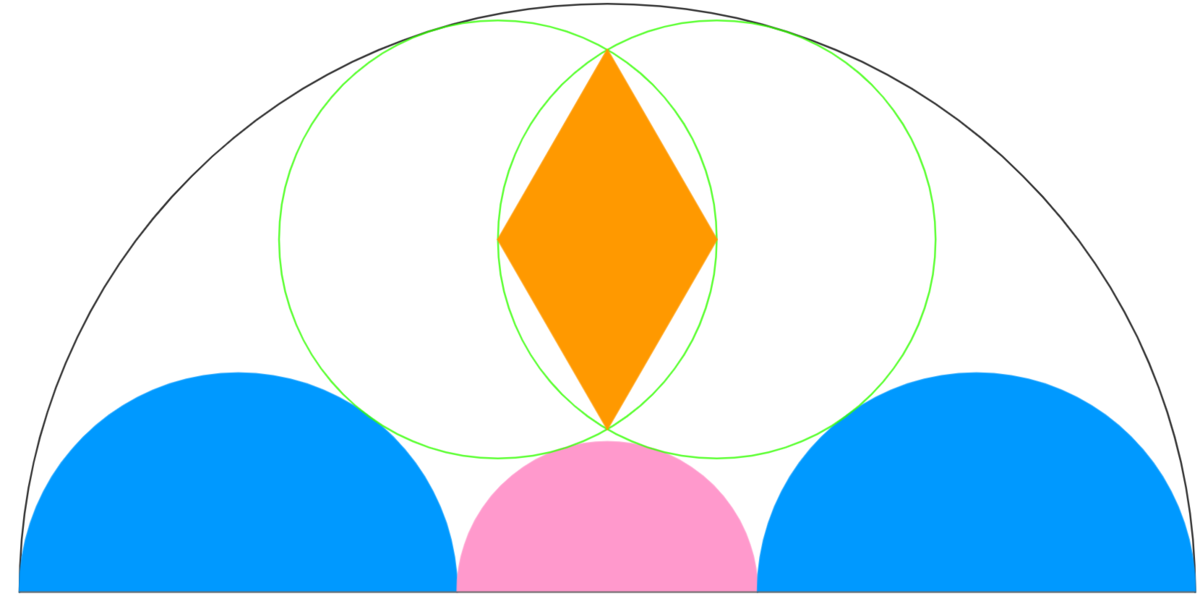
- The diagram shows a black semi-circle with radius 1 .
- The blue semi-circles are equal.
- The green circles interestects such that they pass through each others center.
- The blue and red semi-circles and the green circles are tangent to each other. The green circles and black semi-circle are tangent to each other.
- We use the centers of the green circles and their 2 intersection points to drawn a quadrilateral.
Question : The area of the orange quadrilateral can be expressed as e a b − c d . Evaluate ( e − b ) ( a − c + d )
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
-
We use the pythagorean theorem to solve this problem:
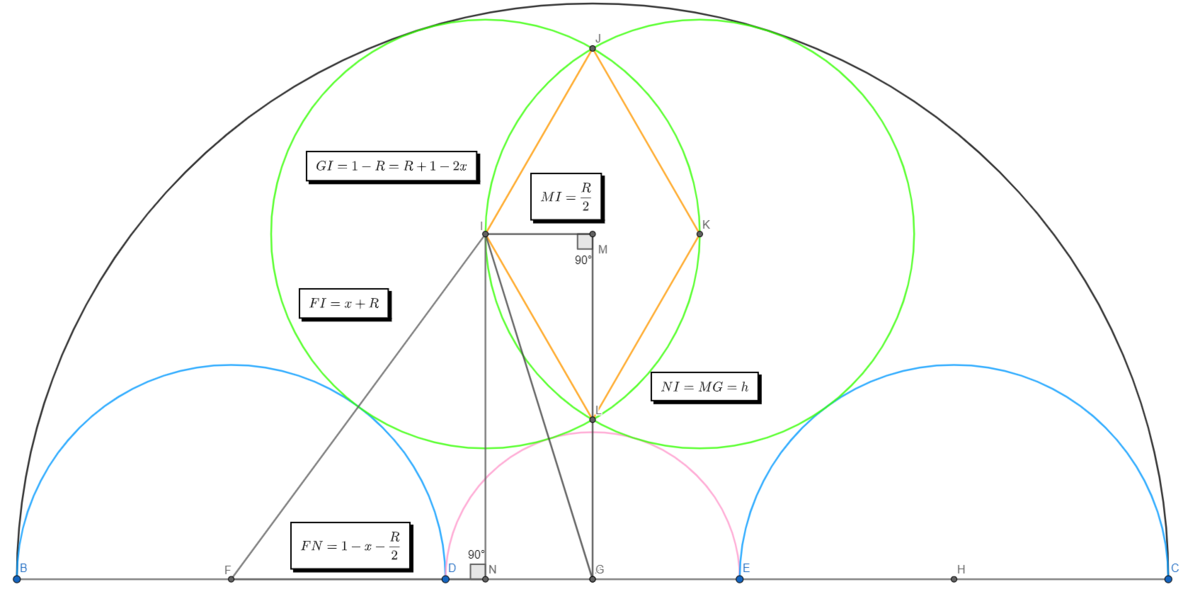
- ⎩ ⎪ ⎨ ⎪ ⎧ ( x + R ) 2 = ( 1 − 2 R − x ) 2 + h 2 ( R + 1 − 2 x ) 2 = ( 2 R ) 2 + h 2 R + 1 − 2 x = 1 − R
- We find x = 2 3 3 − 5 and R = 2 3 3 − 5
- Since the sides of the orange quadrilateral are equal to R , then we have a rhombus
- Then its area is 2 ⋅ 4 3 ( 2 − 5 + 2 3 3 ) 2 = 4 2 9 3 − 1 5 1 1
- Finally ( 4 − 3 ) ( 2 9 − 1 5 + 1 1 ) = 5