My ultimate Sangaku part 3

Geometry Level pending
  • The diagram shows a black semi-circle of radius 1 \boxed{1} .
  • We place a point P \boxed{P} and a point P ′ \boxed{P'} on its diameter.
  • This allows us to draw 3 semi-circles.
  • Since point P \boxed{P} and point P ′ \boxed{P'} can move freely on the diameter as long as there are always 3 semi-circles drawn on the figure, for instance, P ′ \boxed{P'} can not be place to the left side of P \boxed{P}

  • Finally we draw two circles so they are tangent to the black circle, to the middle semi-circle and to one of the 2 other semi-circles.

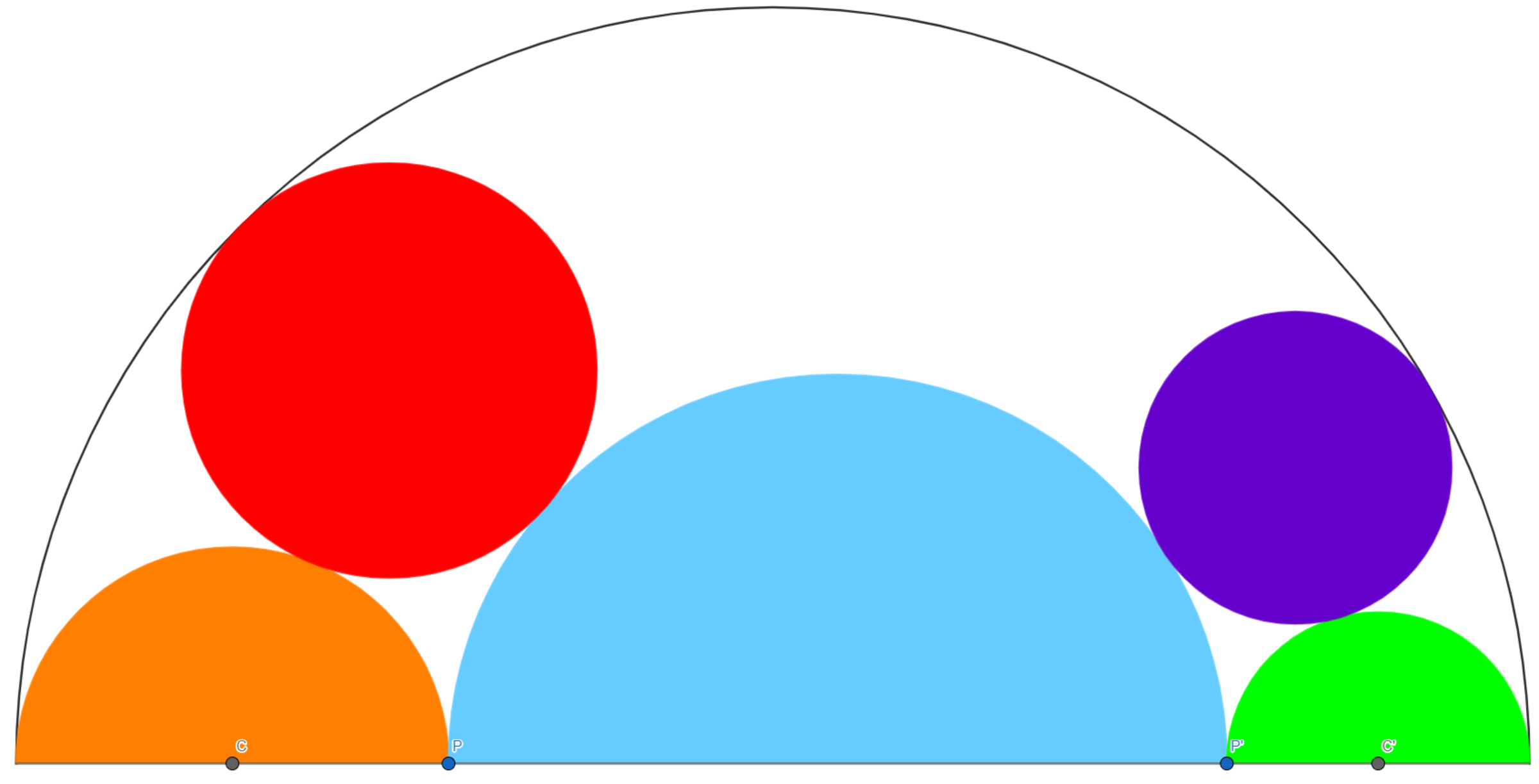
  • The raduis of the orange semi-circle is called x x

  • Depending on the position of P \boxed{P} and P ′ \boxed{P'} , the red and the purple circles can be identical and form a unique pink circle.

Question : When this happens, the area of this pink circle can be written as : a ⋅ x 4 − b ⋅ x 3 + a ⋅ x 2 c ⋅ x 4 + d ⋅ x 2 + c ⋅ π \boxed{\frac{a\cdot x^4-b\cdot x^3+a\cdot x^2}{c\cdot x^4+d\cdot x^2+c}\cdot \pi } where a a , b b , c c and d d are positive integers. Evaluate a + b − c − d \boxed{\sqrt{a+b-c-d}}


The answer is 3.

Valentin Duringer by Valentin Duringer , 30, Belgium

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Valentin Duringer
Aug 24, 2020
  • Let us call the radius of the green semi-circle y y , then the radius of the middle blue semi-circle is 1 − x − y 1-x-y

  • Now we use this diagram and the pythagorean theorem to write some equalities: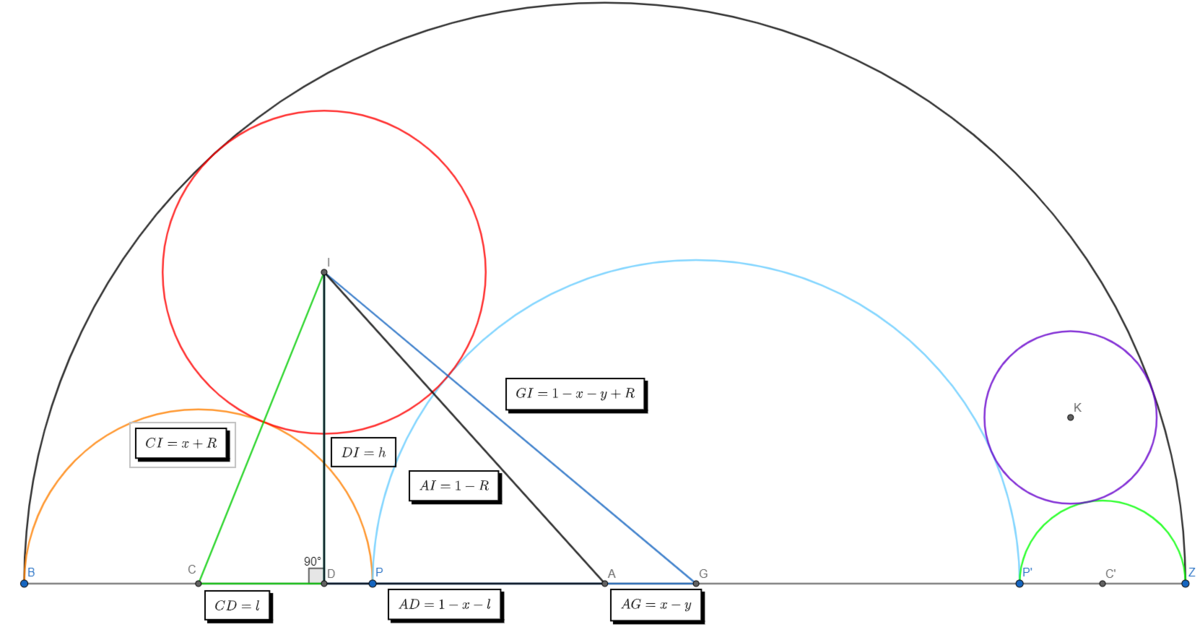

  • { ( x + R ) 2 = l 2 + h 2 ( 1 − x − y + R ) 2 = ( 1 − l − y ) 2 + h 2 ( 1 − R ) 2 = ( 1 − x − l ) 2 + h 2 \begin{cases}\left(x+R\right)^2=l^2+h^2\\\left(1-x-y+R\right)^2=\left(1-l-y\right)^2+h^2\\\left(1-R\right)^2=\left(1-x-l\right)^2+h^2\end{cases}

  • We need to do some algebra to express R ( x ; y ) R(x;y) in terms of x x and y y
  • After some work we find R ( x ; y ) = ( − x + x 2 ) ( − 1 + y ) 1 − x + x 2 − y \boxed{R(x;y)=\frac{\left(-x+x^2\right)\left(-1+y\right)}{1-x+x^2-y}}
  • We can call the radius of the other circle (on the right side) : r ( x ; y ) r(x;y) and its expression in terms of x x and y y is :
  • r ( x ; y ) = ( − y + y 2 ) ( − 1 + x ) 1 − y + y 2 − x \boxed{r(x;y)=\frac{\left(-y+y^2\right)\left(-1+x\right)}{1-y+y^2-x}}
  • If both circles are equal, then R ( x ; y ) = r ( x ; y ) \boxed{R(x;y)=r(x;y)} and after some algebra we find:
  • y = x − 1 x + 1 \boxed{y=\frac{x-1}{x+1}}
  • Now we can express the area of the unique pink circle in terms of x x :
  • R ( x ) = 4 x 4 − 8 x 3 + 4 x 2 x 4 + 2 x 2 + 1 ⋅ π \boxed{R(x)=\frac{4x^4-8x^3+4x^2}{x^4+2x^2+1}\cdot \pi }
  • Finally 4 + 8 − 1 − 2 = 3 \boxed{\sqrt{4+8-1-2}=3}
0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...