My ultimate Sangaku part 4

Geometry Level 5
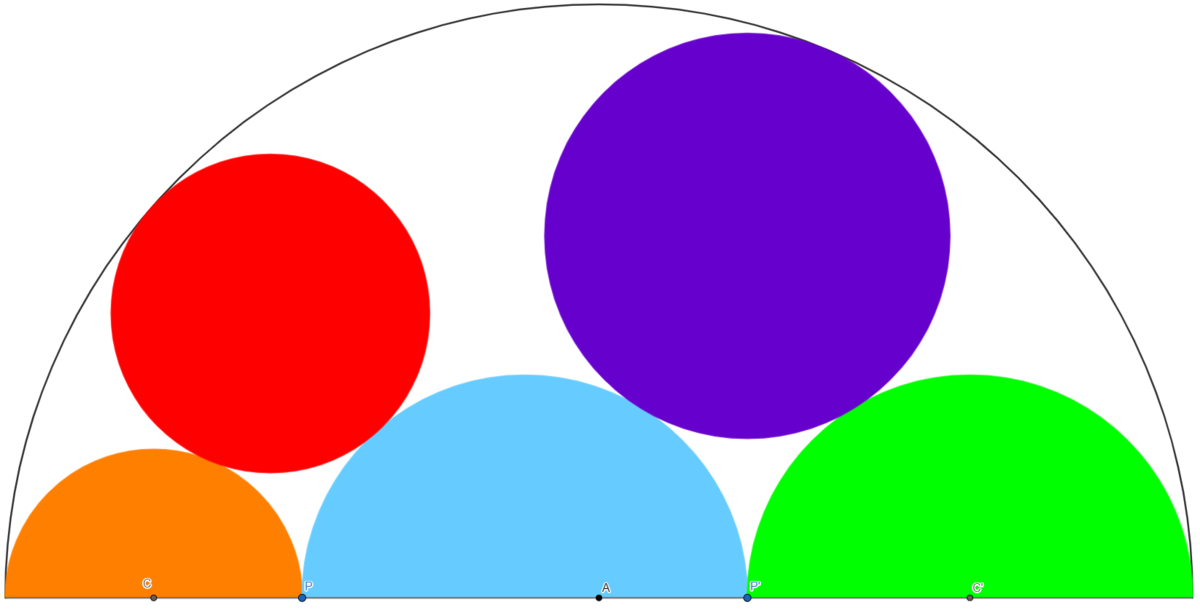
  • The diagram shows a black semi-circle of radius 1 \boxed{1} .
  • We place a point P \boxed{P} and a point P ′ \boxed{P'} on its diameter.
  • This allows us to draw 3 semi-circles.
  • Since point P \boxed{P} and point P ′ \boxed{P'} can move freely on the diameter as long as there are always 3 semi-circles drawn on the figure, for instance, P ′ \boxed{P'} can not be place to the left side of P \boxed{P}
  • Finally we draw two circles so they are tangent to the black circle, to the middle semi-circle and to one of the 2 other semi-circles. Those two circles are red and purple
  • The center of the black semi-circle is the origin of the coordinate system.
  • The center of the red circle is K ( x K , y K ) K\left(x_K,y_K\right) and the center of the purple circle is Q ( x Q , y Q ) Q\left(x_Q,y_Q\right)
  • We give ∣ x K ∣ ∣ x Q ∣ = 31 14 \boxed{\frac{\left|x_K\right|}{\left|x_Q\right|}=\frac{31}{14}} and ∣ y K ∣ ∣ y Q ∣ = 11 14 \boxed{\frac{\left|y_K\right|}{\left|y_Q\right|}=\frac{11}{14}}

Question : The area of the blue middle semi-circle can be expressed as : a b ⋅ π \boxed{\frac{a}{b}\cdot \pi } where a a and b b are positive integers. Evaluate b − a \boxed{b-a}


The answer is 119.

Valentin Duringer by Valentin Duringer , 30, Belgium

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Valentin Duringer
Aug 24, 2020
  • Let us call the radius of the orange semi-circle m m and n n the radius of the green semi-circle , then the radius of the middle blue semi-circle is 1 − m − n 1-m-n

  • Now we use this diagram and the pythagorean theorem to write some equalities: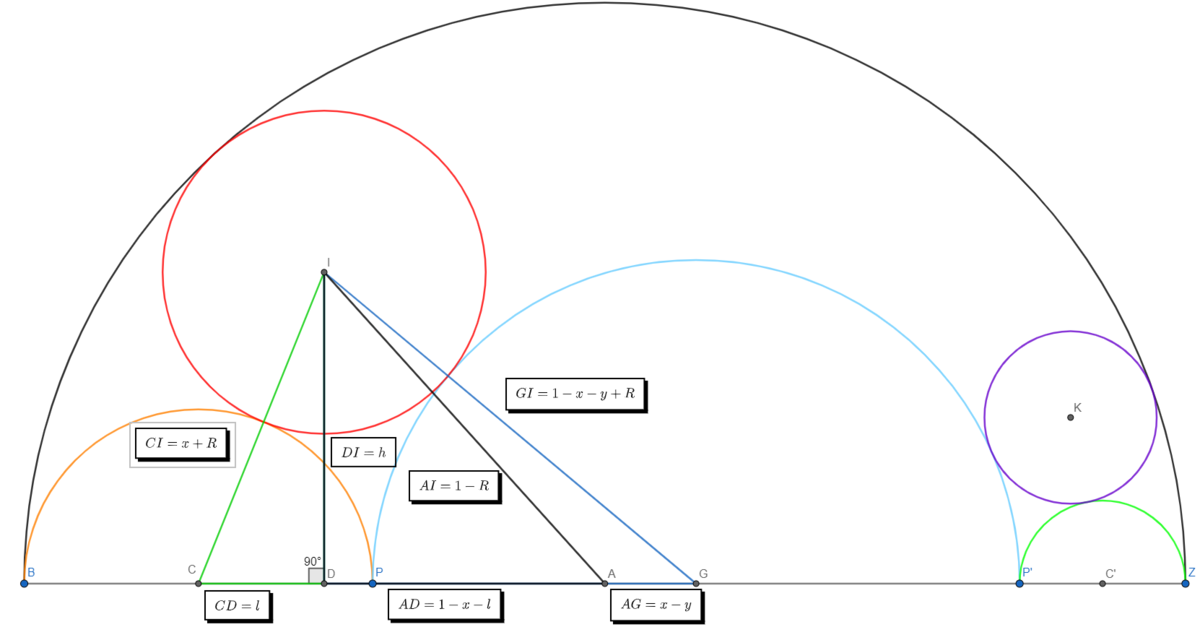 (you can use this diagram made for part 3 for this series, just use m m instead of x x and n n instead of y y

  • { ( m + R ) 2 = l 2 + h 2 ( 1 − m − n + R ) 2 = ( 1 − l − n ) 2 + h 2 ( 1 − R ) 2 = ( 1 − m − l ) 2 + h 2 \begin{cases}\left(m+R\right)^2=l^2+h^2\\\left(1-m-n+R\right)^2=\left(1-l-n\right)^2+h^2\\\left(1-R\right)^2=\left(1-m-l\right)^2+h^2\end{cases}

  • After some algebra we get : l l and h h in terms of m m and n n :
  • l ( m ; n ) = m ( 1 − n ) ( m + 1 ) ( 1 − m + m 2 − n ) − m \boxed{l(m;n)=\frac{m\left(1-n\right)\left(m+1\right)}{\left(1-m+m^2-n\right)-m}}
  • h ( m ; n ) = 2 − ( − 1 + m ) m 2 ( − 1 + n ) ( − 1 + m + n ) ( − 1 + m − m 2 + n ) 2 \boxed{h(m;n)=2\sqrt{\frac{-\left(-1+m\right)m^2\left(-1+n\right)\left(-1+m+n\right)}{\left(-1+m-m^2+n\right)^2}}}
  • Then ∣ x K ∣ = 1 − m ( 1 − n ) ( m + 1 ) 1 − m + m 2 − n \boxed{\left|x_K\right|=1-\frac{m\left(1-n\right)\left(m+1\right)}{1-m+m^2-n}}
  • And ∣ y K ∣ = 2 − ( − 1 + m ) m 2 ( − 1 + n ) ( − 1 + m + n ) ( − 1 + m − m 2 + n ) 2 \boxed{\left|y_K\right|=2\sqrt{\frac{-\left(-1+m\right)m^2\left(-1+n\right)\left(-1+m+n\right)}{\left(-1+m-m^2+n\right)^2}}}
  • x Q \boxed{x_Q} and y Q \boxed{y_Q} have a similar formula as the ones above, you just have to replace m m with n n .
  • Now we can solve the following system of equation in terms of m m and n n :
  • { ∣ x K ∣ ∣ x Q ∣ = 31 14 ∣ y K ∣ ∣ y Q ∣ = 11 14 \begin{cases}\frac{\left|x_K\right|}{\left|x_Q\right|}=\frac{31}{14}\\\frac{\left|y_K\right|}{\left|y_Q\right|}=\frac{11}{14}\end{cases}
  • Solving the system gives us n = 3 8 \boxed{n=\frac{3}{8}} and m = 1 4 \boxed{m=\frac{1}{4}}
  • Then the area of the blue central middle semi-circle is 9 128 ⋅ π \boxed{\frac{9}{128}\cdot \pi }
  • Finally 128 − 9 = 119 \boxed{128-9}=119
0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...