Mysterious point D

Geometry Level 5

Let ABC be a triangle. Let S be the circle through B tangent to CA at A and let T be the circle through C tangent to AB at A. The circles S and T intersect at A and D. Let E be the point where the line AD meets the circumcircle of $\Delta ABC$ .

Find the ratio $\frac{AD}{AE}$ .

If your answer is of the form $\frac{ \sqrt a}{b}$ , where $a$ and $b$ are coprime integers, insert $a + b$ as your answer.

The answer is 3.

2 solutions

Indraneel Mukhopadhyaya
Mar 3, 2017

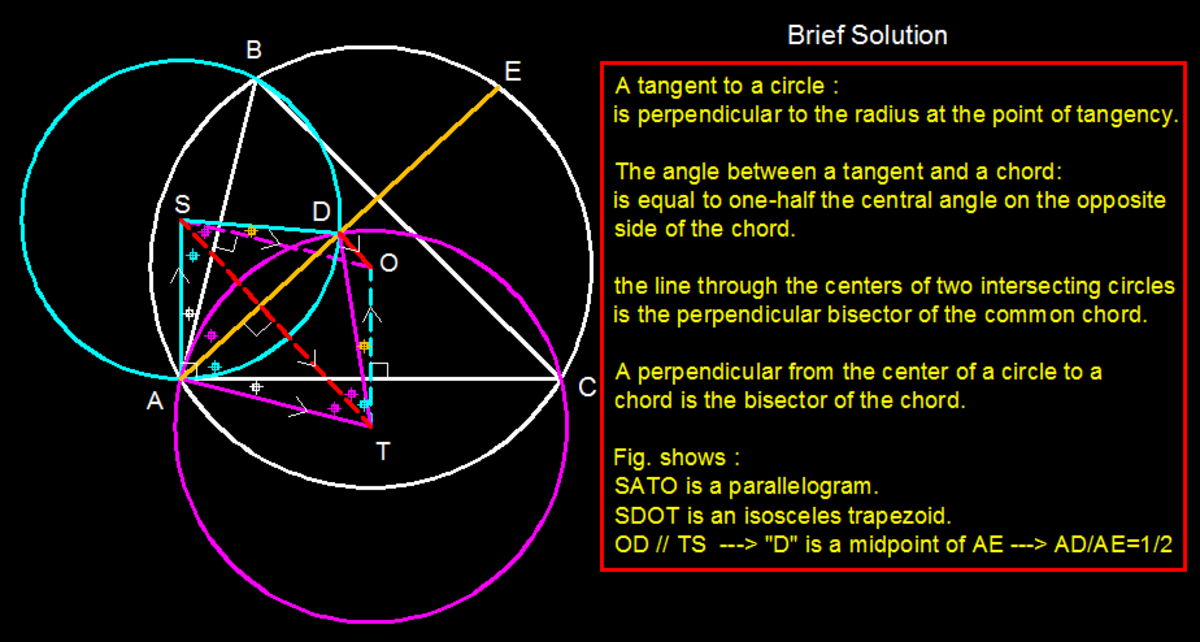
Firstly, we use tangent secant theorem for circles S and T to get : 1) angle CAD=angle ABD and 2) angle BAD=angle ACD respectively.Hence ∆ABD~∆CAD.Hence we get 1) DA bisects angle BDC and 2) AD/CD = BD/AD or we can say AD²=BD.CD ; and by angle sum property in quadrilateral ABDC we get angle BDC= 360-2A.Now,if E is the point where AD meets circle ABC, then angles A and E are supplementary or angle E is 180-A.Clearly angle BDC is greater than angle BEC.Hence, E lies on AD extended.Since ABEC is cyclic 1) angle DEB= angle C and 2) angle DEC=angle B.Also angle EDB=angle EDC=angle A.Hence , we get ∆DEB~∆DCE which implies DE/DC=DB/DE which is same as DE²=BD.CD ; hence we have AD²=DE²=BD.CD which means AD=DE.Therefore, D is the midpoint of AE and AD/AE is 1/2.

I am afraid of reading this. There is an easy method using only and only similarity.

$HINT$ : $\Delta ACD$ ~ $\Delta BCE$ Use similarity in the $\Delta ACD$ and $\Delta BCE$ . AD / BE = AC/BC. Again, Use similarity in the $\Delta BED$ and $\Delta BCA$

Vishwash Kumar ΓΞΩ - 4 years, 3 months ago

Note that what you have written is hint and what I have written is a solution.My solution is exactly the same as yours , involving similarity between 2 pairs of triangles. If someone reads your solution, then he will not understand anything. What makes my solution look long is I have explained every result (as to why those triangles are similar and other results) so that it is simple to understand.

Indraneel Mukhopadhyaya - 4 years, 3 months ago

II nd thing : Are you an IMO aspirant?

Vishwash Kumar ΓΞΩ - 4 years, 3 months ago

This is irrelevant in the context of this question (this is the place to discuss solutions).You may make a separate note if you want to discuss this (or any other) topic with the brilliant users. Just to answer this particular query,I am not an IMO aspirant.

Indraneel Mukhopadhyaya - 4 years, 3 months ago

Ahmad Saad
Mar 5, 2017

Mysterious point D

The answer is 3.

2 solutions

0 pending reports