Mystery in the Middle 2
In a circle puzzle like the one below, the dashed arrows mean to add and the solid arrows mean to multiply:
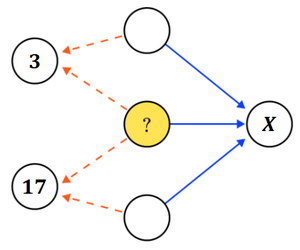
Find the non-zero integer that can replace X so that there are three possible integer values for the question mark.
The answer is -360.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Any better approaches than converting to a sum of squares? It feels a bit clunky.
Log in to reply
I posted my solution, similar to how I solved the bonus question of the inspiration problem . It's a different method, but also feels a bit clunky as I had to test every integer − 3 ≤ r ≤ 1 7 .
Log in to reply
I wondered about (but didn't get far with) a more number theoretical approach; perhaps there's a factorisation that would help? Or maybe some cases fall out modulo a certain number?
If the middle number is x , then the top white circle must be ( 3 − x ) and the bottom white circle must be ( 1 7 − x ) , and ( 3 − x ) x ( 1 7 − x ) = X , which rearranges to x 3 − 2 0 x 2 − 5 1 x − X = 0 .
Suppose that there are three possible integer values p , q , and r for the middle number x . Then by Vieta's Formula , p + q + r = 2 0 , p q + q r + p r = 5 1 , and p q r = X . By substitution, p = − 2 r + 1 0 ± 2 1 − 3 r 2 + 4 0 r + 1 9 6 and q = − 2 r + 1 0 ∓ 2 1 − 3 r 2 + 4 0 r + 1 9 6 .
For p and q to be integers, − 3 r 2 + 4 0 r + 1 9 6 must be a perfect square, and for p and q to be real, − 3 r 2 + 4 0 r + 1 9 6 > 0 , which solves to − 3 ≤ r ≤ 1 7 . Testing each integer r in this range, only r = − 3 , r = 0 , r = 3 , r = 8 , r = 1 5 , and r = 1 7 give perfect squares for − 3 r 2 + 4 0 r + 1 9 6 , and give the following p = − 2 r + 1 0 + 2 1 − 3 r 2 + 4 0 r + 1 9 6 , q = − 2 r + 1 0 − 2 1 − 3 r 2 + 4 0 r + 1 9 6 , and X = p q r values:
| r | p | q | X |
| − 3 | 1 5 | 8 | − 3 6 0 |
| 0 | 1 7 | 3 | 0 |
| 3 | 1 7 | 0 | 0 |
| 8 | 1 5 | − 3 | − 3 6 0 |
| 1 5 | 8 | − 3 | − 3 6 0 |
| 1 7 | 3 | 0 | 0 |
The only non-zero X -value with three possible integer values for the middle number is X = − 3 6 0 .
Let the values in the vertical line of three circles be u , y , v (so y is the question mark).
The equations we have are u + y = 3 , v + y = 1 7 , u v y = x
We want to get an equation for y in terms of x that has three distinct integer roots. Substituting u = 3 − y and v = 1 7 − y : y ( 3 − y ) ( 1 7 − y ) = x
which after tidying becomes y 3 − 2 0 y 2 + 5 1 y − x = 0
This is a cubic in y ; say its three roots are p , q , r . By Vieta, p + q + r = 2 0 , q r + r p + p q = 5 1 , p q r = x
Squaring the first and subtracting twice the second, we get p 2 + q 2 + r 2 = 2 9 8
Since 2 9 8 < 1 8 , this is easy enough to solve; the only triples (up to permutation) that work (together with p + q + r = 2 0 ) are ( 0 , 3 , 1 7 ) and ( − 3 , 8 , 1 5 ) . The first leads to x = 0 , which isn't allowed; hence the answer is − 3 ⋅ 8 ⋅ 1 5 = − 3 6 0 .